Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

8.
\(y=\left(cosx+1\right)^2-1\ge-1\Rightarrow y_{min}=-1\)
\(y=\left(cosx-1\right)\left(cosx+3\right)+3\le3\Rightarrow y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\Rightarrow y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)
15.
Đáp án A đúng
20.
\(-1\le sin\left(\frac{x}{2}+\frac{\pi}{7}\right)\le1\Rightarrow-5\le y\le-1\)
\(y_{max}=-1\) ; \(y_{min}=-5\)

8.
\(y=cos^2x+2\left(2cos^2x-1\right)=5cos^2x-2\)
Do \(0\le cos^2x\le1\Rightarrow-2\le y\le3\)
\(y_{min}=-2;y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\)
\(y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)

4.
\(-1\le sinx\le1\Rightarrow\sqrt{2}\le\sqrt{sinx+3}\le2\)
\(\Rightarrow\sqrt{2}-1\le y\le1\)
12.
ĐKXĐ: \(sinx+1\ne0\Rightarrow sinx\ne-1\Rightarrow x\ne-\frac{\pi}{2}+k2\pi\)
20.
\(y=tanx\) ko xác định khi \(cosx=0\Leftrightarrow x=\frac{\pi}{2}+k\pi\)
22.
\(y_{min}=y\left(\frac{\pi}{4}\right)=cos\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)

a/ \(y=sin2x+\left(\sqrt{3}+1\right)cos2x+sin^2x-cos^2x-1\)
\(=sin2x+\sqrt{3}cos2x-1=2sin\left(2x+\frac{\pi}{3}\right)-1\)
Do \(-1\le sin\left(2x+\frac{\pi}{3}\right)\le1\Rightarrow-3\le y\le1\)
b/ \(y=2sin^2x-2cos^2x-3sinx.cosx-1\)
\(=-2cos2x-\frac{3}{2}sin2x-1=-\frac{5}{2}\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)-1\)
\(=-\frac{5}{2}sin\left(x+a\right)-1\Rightarrow-\frac{7}{2}\le y\le\frac{3}{2}\)
c/ \(y=1-sin2x+2cos2x+\frac{3}{2}sin2x=\frac{1}{2}sin2x+2cos2x+1\)
\(=\frac{\sqrt{17}}{2}\left(\frac{1}{\sqrt{17}}sin2x+\frac{4}{\sqrt{17}}cos2x\right)+1=\frac{\sqrt{17}}{2}sin\left(2x+a\right)+1\)
\(\Rightarrow-\frac{\sqrt{17}}{2}+1\le y\le\frac{\sqrt{17}}{2}+1\)

2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$
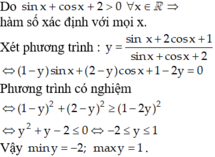
2.
\(0\le\left|sinx\right|\le1\Rightarrow1\le y\le3\)
Min và max lần lượt là 3 và 1
3.
\(cos\left(x-\frac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
8.
\(y=\frac{1}{2}+\frac{1}{2}cos2x+2cos2x=\frac{1}{2}+\frac{5}{2}cos2x\le\frac{1}{2}+\frac{5}{2}.1=3\)
15.
Nó đi qua vô số điểm nên ko có 4 đáp án để chọn thì ko ai có thể trả lời câu này cho bạn cả
18.
\(y=\frac{sinx+2cosx+1}{sinx+cosx+2}\Leftrightarrow y.sinx+y.cosx+2y=sinx+2cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(y-2\right)cosx=1-2y\)
\(\left(y-1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2+2y-4\le0\Rightarrow-2\le y\le1\)
\(\Rightarrow y_{max}=1\)