Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{R_2}=\dfrac{1}{R_{tđ}}-\dfrac{1}{R_1}=\dfrac{1}{3}-\dfrac{1}{6}=\dfrac{1}{6}\)
\(\Rightarrow R_2=6\left(\Omega\right)\)

Điện trở tương đương của đoạn mạch
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{3.6}{3+6}=2\left(\Omega\right)\)
Chúc bạn học tốt

Trong mạch điện mắc song song:
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(\Omega\right)\)
=> Chọn A.
Điện trở tương đương của đoạn mạch
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{3.6}{3+6}=2\left(\Omega\right)\)
⇒ Chọn câu : A
Chúc bạn học tốt

Đáp án D
Điện trở mạch mắc song song
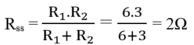
Cường độ dòng điện I = U/R = 6/2 = 3A

\(R_1//R_2\)\(\Rightarrow\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow\dfrac{1}{2,4}=\dfrac{1}{6}+\dfrac{1}{R_1}\)
\(\Rightarrow R_1=4\Omega\)
Ta có \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\) \(\Leftrightarrow2,4=\dfrac{R_16}{R_1+6}\Leftrightarrow2,4\left(R_1+6\right)=6R_1\)
\(\Leftrightarrow2,4R_1+14,4=6R_1\Leftrightarrow-3,6R_1=-14,4\Rightarrow R_1=4\Omega\)

a) Điện trở tương đương của toàn mạch :
\(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{4.6}{4+6}=2,4\left(\Omega\right)\)
b) Có : \(U=U_1=U_2=6\left(V\right)\) (vì R1 // R2)
Cường độ dòng điện trở R1 :
\(I_1=\dfrac{U_1}{R_1}=\dfrac{6}{4}=1,5\left(A\right)\)
Cường độ dòng điện qua mạch chính :
\(I=\dfrac{U}{R_{tđ}}=\dfrac{6}{2,4}=2,5\left(A\right)\)
Chúc bạn học tốt

a,\(\Rightarrow I1=Im-I2=1,2-0,4=0,8A\)
b,\(\Rightarrow U1=I1R1=4,8V\)
c,\(\Rightarrow R2=\dfrac{U1}{I2}=12\Omega\)
d,\(\Rightarrow Rtd=\dfrac{R1R2}{R1+R2}=4\Omega\)

a, CĐDĐ qua R1 :
Ta có: \(I=I_1+I_2\Leftrightarrow I_1=I-I_2=1,2-0,4=0,8\left(A\right)\)
b, HĐT giữa 2 đầu R1:
Ta có: \(I_1=\dfrac{U_1}{R_1}\Leftrightarrow U_1=I_1.R_1=0,8.6=4,8\left(V\right)\)
c, Điện trở R2:
\(R_2=\dfrac{U_2}{I_2}=\dfrac{U_1}{I_2}=\dfrac{4,8}{0,4}=12\left(\Omega\right)\)
d, Điện trở tđ của mạch:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{6.12}{6+12}=4\left(\Omega\right)\)
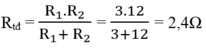
\(R_{td}\)=\(\frac{R_1.R_2}{R_1+R_2}\)=\(\frac{3.6}{3+6}\)=2\(\Omega\)