Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔOBA vuông tại B có sin BAO=OB/OA=1/2
nên góc BAO=30 độ
Xét ΔOBI có OB=OI và góc BOI=60 độ
nên ΔOBI đều
=>OI=OB=1/2OA
=>AI*AO=2R^2
Xét ΔBDE vuông tại D có DC vuông góc BE
nên ΔBDE vuông tại D
=>BC*BE=BD^2=4R^2
=>BC*BE+AI*AO=6R^2

a) Ta có: Đường tròn (O;R) có đường kính CD và điểm A nằm trên cung CD => ^CAD=900
=> ^PAQ=900 => \(\Delta\)APQ vuông tại A
Do PQ là tiếp tuyến của (O) tại B => AB là đường cao của \(\Delta\)APQ
=> ^PAB=^AQP (Cùng phụ ^APQ) hay ^CAO=^DQP
Mà \(\Delta\)AOC cân tại O => ^CAO=^ACO => ^DQP=^ACO
Lại có: ^ACO+^PCD=1800 => ^DQP+^PCD=1800
=> Tứ giác CPQD nội tiếp đường tròn (đpcm).
b) Xét \(\Delta\)APQ vuông tại A: Có đường trung tuyến AI => \(\Delta\)AIQ cân tại I
=> ^IAQ=^IQA hay ^IAQ=^DQP => ^IAQ=^ACO (Do ^DQP=^ACO)
Hay ^IAQ=^ACD. Mà ^IAQ+^CAI=900 => ^ACD+^CAI=900
=> AI vuông góc với CD (đpcm).
c) Ta thấy tứ giác CPQD nội tiếp đường tròn
=> 4 đường trung trực của CP;CD;DQ;PQ cắt nhau tại 1 điểm (1)
E là tâm đường tròn ngoại tiếp \(\Delta\)CPQ => Trung trực của CP và CD cắt nhau tại E (2)
Từ (1) và (2) => Điểm E nằm trên trung trực của PQ.
Lại có: I là trung điểm PQ => E là điểm cách PQ 1 khoảng bằng đoạn EI (*)
AB vuông góc PQ; EI cũng vuông góc PQ => AB//EI hay AO//EI (3)
E thuộc trung trực CD; O là trung điểm CD => OE vuông góc CD.
Mà AI vuông góc CD => OE//AI (4)ư
Từ (3) và (4) => Tứ giác AOEI là hình bình hành => AO=EI (**)
Từ (*) và (**) => E là điểm cách PQ 1 khoảng bằng đoạn AO
Mà AO là bk của (O); PQ là tiếp tuyến của (O) tại B
Nên ta có thể nói: Điểm E là điểm cách tiếp tuyến của (O) tại B một khoảng bằng độ dài bán kính của (O)
Vậy khi đường kính CD thay đổi thì điểm E di động trên đường thẳng song song với tiếp tuyến tại B của đường tròn (O) và cách (O) 1 khoảng bằng độ dài bk của (O).

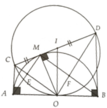
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

1: góc EAO+góc EDO=180 độ
=>EAOD nội tiếp
2: Xét (O) có
EA,ED là tiếp tuyến
=>EA=ED
mà OA=OD
nên OE là trung trực của AD
=>OE vuông góc AD tại H
góc AKB=1/2*sđ cug AB=90 độ
=>AK vuông góc EB
ΔEAB vuông tại E có AK vuông góc EB
nên EK*EB=EA^2=EH*EO
=>EK/EO=EH/EB
=>ΔEKH đồng dạng với ΔEOB
=>góc EHK=góc EBO=góc KBA

Hình bạn tự vẽ rồi nhâ
từ câu a) ta thấy AB là tiếp tuyến của đường tròn (J) đường kính CD
gọi P,Q lần lượt là giao của AD và (O),BC và (J)
có góc APB=CQD=90 độ (góc nt chắn nx đg tròn)
=>góc DPB= góc BQD=90 độ
=>tugiac BQPD là tgnt =>góc PDB= góc PQI(1)
Vì AC//BD nên góc PDB=góc IAC(2)
từ (1) và (2) =>góc PQI= góc IAC
=>tgPQI đồng dạng tgCAI(g.g)
=>PI/CI=QI/AI
=>IP.IA=IC.IQ
=>phương tích của điểm I đối vs (O) và (J) = nhau
=>I nằm trên trục đẳng phương EF của 2 đg tròn
Vậy I,E,F thằng hàng(dpcm)