CHỦ ĐỀ PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Bài 1) Viết PTTQ của đường thẳng d
a) Qua M(-1;-4) và song song với đường thẳng 3x+5y-2=0
b) Qua N(1;1) và vuông góc với đường thẳng 2x+3y+7=0
Bài 2) Viết PT đường thẳng đi qua M(2;5) và cách đều hai điểm P(-1;2),Q(5;4)
Bài 3) Cho đường thằng d1: 2x-y-2=0 ; d2: x+y+3=0 và điểm M(3;0). Viết phương trình đường thẳng D đi qua M, cắt d1 và d2 lần lượt tại điểm A và B sao cho M là trung điểm của đoạn thẳng AB.
Bài 4) Cho tam giác ABC biết A(2;1) B(-1;0) C(0;3)
a) Viết PTTQ của đường cao AH
b)Viết PTTQ của đường trung trực của đoạn thẳng AB
c) Viết PTTQ của đường thẳng BC
d) Viết PTTQ của đường thẳng qua A và song song với đường thẳng BC
Bài 5) Trong mặt phẳng với hệ tọa độ Oxy, viết phương trình đường thẳng \(\Delta\) song song với đường thẳng d: 3x-4y+1=0 và cách d một khoảng bằng 1
Bài 6) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC biết phương trình cạnh BC: x-2y+5=0, phương trình đường trung tuyến BB': y-2=0 và phương trình đường trung tuyến CC': 2x-y-2=0. Tìm tọa độ các đỉnh của tam giác.
Bài 7) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thằng d1: x-y-4=0 , d2: 2x=y-2=0 và 2 điểm A(7;5) B(2;3). Tìm điểm C trên đường thẳng d1 và điểm D trên đường thằng d2 sao cho tứ giác ABCD là hình bình hành.
Bài 8) Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm I(6;2) là giao điểm của hai đường chéo AC và BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm A của cạnh CD thuộc đường thằng d: x+y-5=0. Viết phương trình đường thẳng AB.
CHỦ ĐỀ ĐƯỜNG TRÒN:
Bài 9) Trong mặt phẳng với hệ tọa độ Oxy, cho đường thằng d: 2x-y-5=0 và hai điểm A(1;2) B(4;1). Viết phương trình đường tròn (C) có tâm thuộc d và đi qua hai điểm A,B
Bài 10) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1: x+3y+8=0, d2: 3x-y+10=0 và điểm A(-2;1). Viết phương trình đường tròn (C) có tâm thuộc d1 đi qua điểm A và tiếp xúc với d2
Bài 11) Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(-1;1) B(3;3) và đường thẳng d: 3x-y+8=0. Viết phương trình đường tròn (C) đi qua hai điểm A,B và tiếp xúc với d
Bài 12) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d: x+2y-3=0 và \(\Delta\): x+3y-5=0. Viết phương trình đường tròn (C) có bán kính bằng \(\frac{2\sqrt{10}}{5}\), có tâm thuộc d và tiếp xúc với \(\Delta\)
Bài 13) Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): \(\left(x-1\right)^2+\left(y-2\right)^2=8\)
a) Viết phương trình tiếp tuyến của đường tròn (C) tại điểm A(3;-4)
b) Viết phương trình tiếp tuyến của đường tròn (C) đi qua điểm B(5;-2)
c) Viết phương trình tiếp tuyến của đường tròn (C), biết tiếp tuyến vuông góc với đường thẳng d: x+y+2014=0
d) Viết phương trình tiếp tuyến của đường tròn (C), biết tiếp tuyến tạo với trục tung một góc 45 độ
CHỦ ĐỀ ELIP
Bài 14) Xác định các đỉnh, độ dài các trục, tiêu cự, tiêu điểm, tâm sai của elip có phương trình sau:
a) \(\frac{x^2}{2}+\frac{y^2}{2}=1\)
b) \(4x^2+25y^2=100\)
Bài 15) Lập phương trình chính tắc của Elip, biết
a) Elip đi qua điểm M\(\left(2;\frac{5}{3}\right)\) và có một tiêu điểm F1(-2;0)
b) Elip nhận F2(5;0) là một tiêu điểm và có độ dài trục nhỏ bằng \(4\sqrt{6}\)
c) Elip có độ dài trục lớn bằng \(2\sqrt{5}\) và tiêu cự bằng 2.
d) Elip đi qua hai điểm M(2;\(-\sqrt{2}\)) và N\(\left(-\sqrt{6};1\right)\)
Bài 16) Lập phương trình chính tắc của Elip, biết:
a) Elip có tổng độ dài hai trục bằng 8 và tâm sai \(e=\frac{1}{\sqrt{2}}\)
b) Elip có tâm sai \(e=\frac{\sqrt{5}}{3}\) và hình chữ nhật cơ sở có chu vi bằng 20.
c) Elip có tiêu điểm F1(-2;0) và hình chữ nhật cơ sở có diện tích bằng \(12\sqrt{5}\)

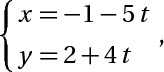 d2:
d2: 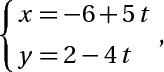
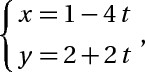 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
Sử dụng công thức trung điểm thôi bạn: lấy hoành độ cộng lại chia đội, tung độ cộng lại chia đôi
Thao Nhi Nguyen
1. b/
Do M thuộc d nên tọa độ có dạng \(M\left(3m+1;2-4m\right)\Rightarrow\overrightarrow{AM}=\left(3m+1;-1-4m\right)\)
\(AM=\sqrt{\left(3m+1\right)^2+\left(-1-4m\right)^2}=5\)
\(\Leftrightarrow\left(3m+1\right)^2+\left(4m+1\right)^2=25\)
\(\Leftrightarrow25m^2+14m-23=0\Rightarrow\left[{}\begin{matrix}m=\frac{-7+4\sqrt{39}}{25}\\m=\frac{-7-4\sqrt{39}}{25}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}M\left(\frac{4+12\sqrt{39}}{25};\frac{78-16\sqrt{39}}{25}\right)\\M\left(\frac{4-12\sqrt{39}}{25};\frac{78+16\sqrt{39}}{25}\right)\end{matrix}\right.\)
Số xấu quá
2. \(\overrightarrow{AB}=\left(-4;8\right)=-4\left(1;-2\right)\)
Gọi I là trung điểm AB \(\Rightarrow I\left(4;-1\right)\)
Phương trình trung trực d' của AB nhận \(\left(1;-2\right)\) là vtpt có dạng:
\(1\left(x-4\right)-2\left(y+1\right)=0\Leftrightarrow x-2y-6=0\)
M là giao điểm d và d' nên tọa độ thỏa: \(\left\{{}\begin{matrix}x+3y+4=0\\x-2y-6=0\end{matrix}\right.\) \(\Rightarrow M\left(2;-2\right)\)