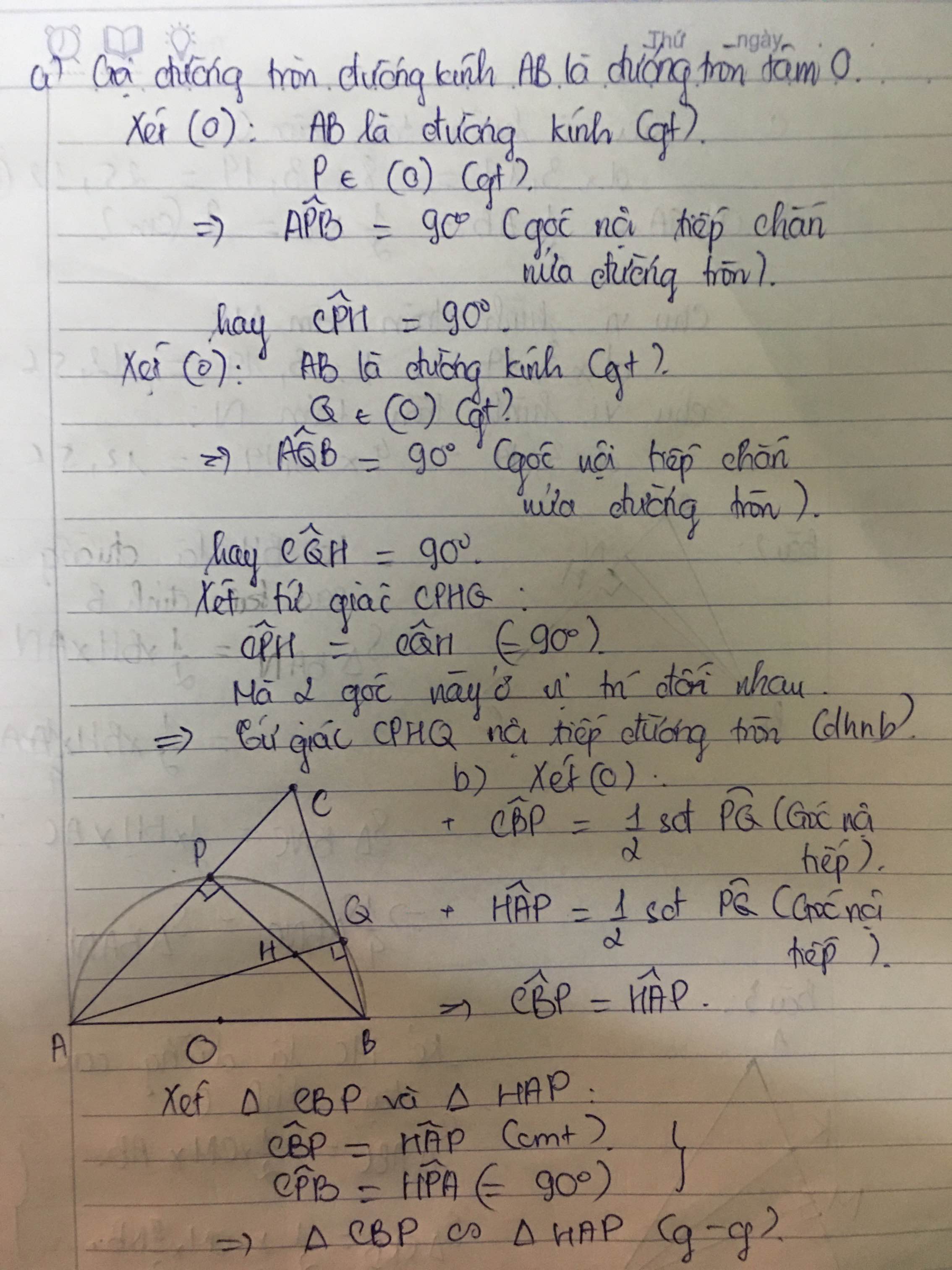Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc APB=góc AQB=1/2*180=90 độ
=>AQ vuông góc BC, BP vuông góc CA
góc CPH+góc CQH=180 độ
=>CPHQ nội tiếp

a. Em tự giải
b.
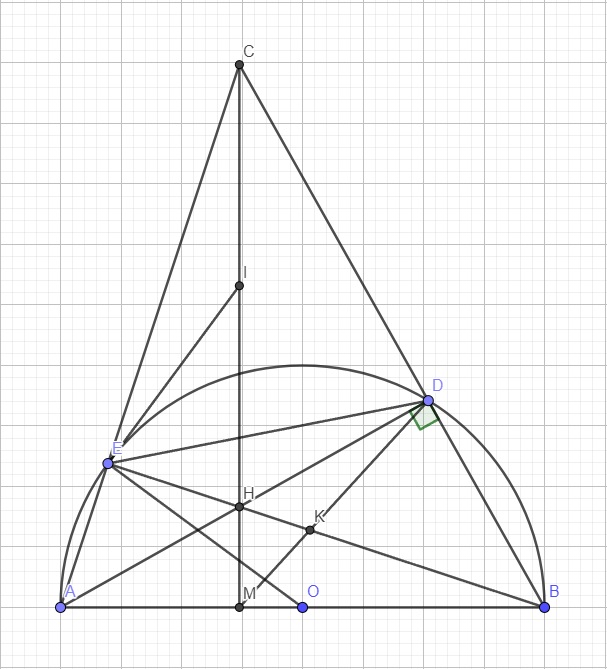
Do tứ giác BDHM nội tiếp \(\Rightarrow\widehat{HDM}=\widehat{HBM}\) (cùng chắn cung HM)
Do tứ giác ABDE nội tiếp \(\Rightarrow\widehat{HBM}=\widehat{ADE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{HDM}=\widehat{ADE}\)
\(\Rightarrow DH\) là phân giác trong góc \(\widehat{EDK}\) của tam giác EDK
Lại có \(DH\perp DB\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow DB\) là phân giác ngoài góc \(\widehat{EDK}\) của tam giác EDK
Áp dụng định lý phân giác:
\(\dfrac{EH}{HK}=\dfrac{EB}{BK}=\dfrac{ED}{DK}\) \(\Rightarrow BK.HE=BE.HK\)
c.
Hai điểm D và E cùng nhìn CH dưới 1 góc vuông nên tứ giác CDHE nội tiếp đường tròn đường kính CH
\(\Rightarrow I\) là trung điểm CH
Trong tam giác ABC, do hai đường cao AD và BE cắt nhau tại H \(\Rightarrow H\) là trực tâm
\(\Rightarrow CH\perp AB\) hay C;H;M thẳng hàng
Ta có \(IC=IE\) (do I là tâm đường tròn ngoại tiếp CDE) \(\Rightarrow\Delta CIE\) cân tại I
\(\Rightarrow\widehat{ECI}=\widehat{CEI}\)
Lại có \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O \(\Rightarrow\widehat{OBE}=\widehat{OEB}\)
Mà \(\widehat{OBE}=\widehat{ECI}\) (cùng phụ \(\widehat{BAC}\))
\(\Rightarrow\widehat{CEI}=\widehat{OEB}\)
\(\Rightarrow\widehat{CEI}+\widehat{IEB}=\widehat{OEB}+\widehat{IEB}\)
\(\Rightarrow\widehat{CEB}=\widehat{OEI}\)
\(\Rightarrow\widehat{OEI}=90^{ }\)
Hay \(OE\perp IE\Rightarrow IE\) là tiếp tuyến của đường tròn tâm O

O B A C M N P Q I K
a) Do AMNP là hình vuông nên \(\widehat{QMB}=45^o\)
Lại có do C là điểm chính giữa của nửa đường tròn nên \(\widebat{CB}=90^o\Rightarrow\widehat{CMB}=45^o\)
(Góc nội tiếp)
Vậy thì \(\widehat{CMQ}=\widehat{CMB}+\widehat{BMQ}=45^o+45^o=90^o\)
Vậy CQ là đường kính hay C và Q đối xứng nhau qua O.
b) Ta thấyAMNP là hình vuông. MI là phân giác góc \(\widehat{AMB}\) nên \(\Delta MAI=\Delta MNI\left(c-g-c\right)\Rightarrow\widehat{MAI}=\widehat{MNI}\)
Lại có \(\widehat{MAI}=\widehat{IAM}\) nên \(\widehat{MNI}=\widehat{IAM}\)
Xét tứ giác AINB có \(\widehat{MNI}=\widehat{IAM}\) nên AINB là tứ giác nội tiếp (góc ngoài tại đỉnh bằng góc đối diện)