
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2) \(B=\left(1-2-3+4\right)+\left(5-6-7+8\right)+...+\left(1989-1990-1991+1992\right)+1993-1994\)
\(=0+0+...+0+1993-1994=0+1993-1994=-1\)

\(B=\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)+1\)
\(=\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}+\dfrac{2022}{2022}\)
=2022(1/2+1/3+...+1/2021+1/2022)
=>B/A=2022

\(A=1-3+5-7+......-2019+2021-2023\)
\(A=\left(1-3\right)+\left(5-7\right)+....+\left(2021-2023\right)\)
\(A=-2+\left(-2\right)+....+\left(-2\right)\left(506 cặp\right)\)
\(A=-2.506\)
\(A=-1012\)
*) A=(1-3)+(5-7)+....+(2021-2023)
<=> A=-2+(-2)+...+(-2)
Dãy A có (2023-1):2+1=1012 số số hạng
=> Có 506 số (-2)
=> A=(-2).506=-1012

Tính P = 11+2+11+2+3+11+2+3+4+...+11+2+3+4+...+2021
Chúc bạn học tốt nhé
P=1+1/3+1/6+1/10+…..+1/2021×2022÷2
P/2=1/2+1/6+1/12+1/20+…..+1/2021×2022
P/2=1/1×2+1/2×3+1/3×4+…….+1/2021×2022
P/2=1-1/2+1/2-1/3+1/3-1/4+….+1/2021-1/2022=1-1/2022=2021/2022
P=2021/1011
Chúc bn học tốt

P=[(1-2)+(-3+4)+(5-6)+(-7+8)+...+(993-994)+(-995+996)]+997
P=[(-1)+1+(-1)+1+...+(-1)+1+(-1)+1]+997
P= 0 +0 +...+ 0 +997
P=997
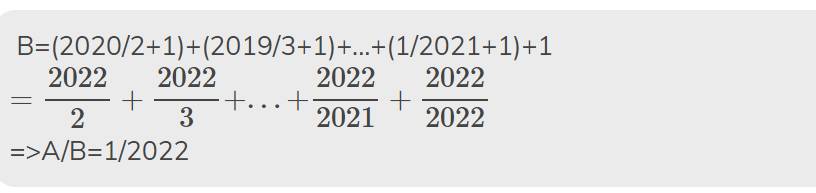
a) Ta có: \(1+\left(-2\right)+3+\left(-4\right)+...+2021\)
\(=\left(1-2\right)+\left(3-4\right)+...+\left(2019-2020\right)+2021\)
\(=\left(-1\right)+\left(-1\right)+...+\left(-1\right)+2021\)
\(=-1010+2021=1011\)