Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Công thức về khối lượng phản ứng:
mCaCO3 = mCaO + mCO2
b) mCaCO3 = 280 + 110 = 390 kg
=> %CaCO3
= \(\frac{390}{560}\) = 69,7%

a) mCaCO3 = mCaO + mCO2
b) Khối lượng của CaCO3 đã phản ứng:
140 + 110 = 250 kg
Tỉ lệ phần trăm khối lượng CaCO3 chứa trong đá vôi:
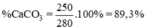

Sơ đồ : Canxi cacbonat → canxi oxit + khí cacbonic
Áp dụng ĐLBTKL cho sơ đồ trên ta có :
m c a n x i c a c b o n a t = m c a n x i o x i t + m k h í c a c b o n i c m k h í c a c b o n i c = m c a n x i c a c b o n a t - m c a n x i o x i t = 5 – 2 , 8 = 2 , 2 ( t ấ n )

PTHH: CaCO3 -to-> CaO + CO2
Theo PT: __________56(g)__44(g)
Theo đề: __________?(tấn)__0,44(tấn)
=> mCaO= (56.0,44)/44= 0,56(tấn)

a) Công thức về khối lượng phản ứng:
mCaCO3 = mCaO + mCO2
b) Áp dụng định luật bảo toàn khối lượng ta có :
mCaCO3 = 140 + 110 = 250 kg
Tỉ lệ phần trăm của Canxi cacbonat có trong đá vôi là :
%mCaCO3 = \(\frac{250.100\text{%}}{280}\) = 89,28%.

a/ PTHH: CaCO3 \(\underrightarrow{nung}\) CaO + CO2
b/Áp dụng định luật bảo toàn khối lương, ta có:
mCaCO3 = mCO2 + mCaO = 110 + 150 = 250kg
c/ %mCacO3 = \(\frac{250}{280}\) x 100% = 89,3%
Chúc bạn học tốt!!!

\(a.\)
\(m_{CaCO_3}=150\cdot80\%=120\left(g\right)\)
\(n_{CaCO_3}=\dfrac{120}{100}=1.2\left(mol\right)\)
\(CaCO_3\underrightarrow{^{^{t^0}}}CaO+CO_2\)
\(1.2...........1.2\)
\(m_{CaO=}=1.2\cdot56=67.2\left(g\right)\)
\(b.\)
\(n_{CO_2}=\dfrac{27.6}{24}=1.15\left(mol\right)\)
\(n_{CaCO_3}=1.15\left(mol\right)\)
\(m_{CaCO_3}=1.15\cdot100=115\left(g\right)\)
\(m_{TC}=115\cdot20\%=23\left(g\right)\)
a, - Khối lượng CaCO3 trong 150g đá là : 120g
=> \(n_{CaCO3}=\dfrac{m}{M}=1,2\left(mol\right)\)
\(PTHH:CaCO_3\rightarrow CaO+CO_2\)
Theo PTHH : \(n_{CaO}=1,2\left(mol\right)\)
\(\Rightarrow m_{vs}=m_{CaO}=n.M=67,2\left(g\right)\)
b, \(n_{CO2}=\dfrac{V}{24}=1,15\left(mol\right)\)
Theo PTHH : \(n_{CaCO3}=1,15\left(mol\right)\)
\(\Rightarrow m_{CaCO3}=n.M=115\left(g\right)\)
=> %Tạp chất là : \(\left(1-\dfrac{115}{150}\right).100\%=\dfrac{70}{3}\%\)
Vậy ...

\(1,PTHH:CaCO_3\underrightarrow{t^o}CaO+CO_2\)
\(áp,dụng.dlbtkl,ta.có:\)
\(m_{CaCO_3}=m_{CaO}+m_{CO_2}\\ m_{CO_2}=m_{CaCO_3}-m_{CaO}=5-2,8=2,2\left(g\right)\)
\(2,a,pthh:4P+5O_2\underrightarrow{t^o}P_2O_5\)
\(n_P=\dfrac{m}{M}=\dfrac{12.4}{31}=0,4\left(mol\right)\)
\(b,theo.pthh\Rightarrow n_{O_2}=\dfrac{5}{4}n_P=\dfrac{5}{4}.0,4=0,5\left(mol\right)\\ \Rightarrow V_{O_2}=n.22,4=0,5.22,4=11,2\left(l\right)\\ m_{O_2}=n.M=0,5.32=16\left(g\right)\)
1. Áp dụng ĐLBTKL, ta có:
\(m_{CaCO_3}=m_{CaO}+m_{CO_2}\)
\(\Leftrightarrow5=2,8+m_{CO_2}\)
\(\Leftrightarrow m_{CO_2}=5-2,8=2,2\left(g\right)\)
2. Ta có: \(n_P=\dfrac{12,4}{31}=0,4\left(mol\right)\)
a. \(PTHH:4P+5O_2\overset{t^o}{--->}2P_2O_5\)
b. Theo PT: \(n_{O_2}=\dfrac{5}{4}.n_P=\dfrac{5}{4}.0,4=0,5\left(mol\right)\)
Theo PT: \(n_{P_2O_5}=\dfrac{1}{2}.n_P=\dfrac{1}{2}.0,4=0,2\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}V_{O_2}=0,5.22,4=11,2\left(lít\right)\\m_{P_2O_5}=0,2.142=28,4\left(g\right)\end{matrix}\right.\)