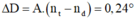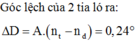Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định luật khúc xạ ánh sáng
\(1.\sin30^0=n_đ.\sin r_đ\)
\(1.\sin30^0=n_t.\sin r_t\)
=> \(r_đ=22,12^0,r_t=21,858^0\)
Góc lệch giữa tia đỏ và tím là \(r_đ-r_t=0,2624^0.\)

Ta xét 1 bất biến rất thú vị như sau:
Ta viết số các bông hoa trong mỗi nhóm dưới dạng nhị phân:
\(1=1_2\), \(2=10_2\), \(3=11_3\) và tổng S của các số này được tính theo quy tắc sau:
\(S=01+10+11=00\) (nếu hàng có chẵn số 1 thì KQ bằng 0 còn nếu có lẻ số 1 thì KQ bằng 1)
Ta có 2NX:
NX1: Nếu đến lượt chơi của 1 người nào đó mà tổng S đang bằng 0 thì do dù có chơi như thế nào, tổng S cũng sẽ khác 0.
NX2: Nếu đến lượt chơi của 1 người nào đó mà tổng S đang khác 0 thì luôn có 1 nước đi cho người đó để đưa tổng S về lại bằng 0. (đây chính là chiến thuật để thắng trò chơi)
Trong trò chơi này, ta thấy tổng S ban đầu bằng 0 nên theo NX1, dù An có bốc như thế nào thì tổng S cũng sẽ khác 0. Kế đó, sử dụng NX2, Bình luôn có thể bốc để cho tổng S về lại bằng 0 và cứ tiếp tục như thế, Bình là người sẽ đưa được số sỏi về trạng thái (0,0,0) (vì khi đó \(S=0\))
Cuối cùng là số hoa chứ không phải số sỏi đâu. Trò chơi này chính là 1 phiên bản của trò chơi Nim, bạn có thể tìm hiểu trên mạng.

Dựa vào định luật khúc xạ ánh sáng ( từ lăng kính ra không khí ).
\(n.\sin r = 1.\sin i \)
n là chiết suất của lăng kính đối với ánh sáng tím.
góc r cùng nhau, i lớn khi n lớn. ( do 00 < i < 900)

Nguyên tắc ở đây, khi chiếu tia sáng từ nước ra không khí thì so với phương tia tới, tia đỏ lệch ít nhất, tia tím lệch nhiều nhất.
Do tia lục đi là là mặt nước nên tia da cam, vàng ló ra khỏi mặt nước, còn tia lam, chàm, tím bị phản xạ toàn phần.
Theo như các phương án của bạn, thì đáp án A là đúng nhất.

Chọn D
sin i 1 = sin D min + A 2 = n sin A 2 ⇒ sin i 1 = 1 , 635 sin 40 ° 2 ⇒ i 1 = 34 °