Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì 2 vế ko âm nên bình phương cả 2 vế ta dc :
\(\left|x+y\right|^2\le\left|x\right|^2+\left|y\right|^2\)
\(\Rightarrow\left(x+y\right).\left(x+y\right)\le\left(\left|x\right|+\left|y\right|\right)\left(\left|x\right|+\left|y\right|\right)\)
\(\Rightarrow x^2+2xy+y^2\le x^2+2\left|x\right|\left|y\right|+y^2\)
\(\Rightarrow xy\le\left|xy\right|\) (Luôn đúng với mọi \(x,y\))
Vậy bất đẳng thức trên đúng. Dấu "=" xảy ra khi \(\left|xy\right|=xy\) \(\Leftrightarrow x,y\) cùng dấu
Vậy \(\left|x+y\right|\le\left|x\right|+\left|y\right|\rightarrowđpcm\)
b) Áp dụng câu a ta có :
\(\left|x-y\right|+\left|y\right|\ge\left|x-y+y\right|=\left|x\right|\Rightarrow\left|x-y\right|\ge\left|x\right|-\left|y\right|\)
Vậy \(\left|x-y\right|\ge\left|x\right|-\left|y\right|\rightarrowđpcm\)

vậy f(1/2)+3.f(2)=1/4 hay 3f(1/2)+9.f(2)=3/4
và f(2)+3.f(1/2)=4
trừ vế theo vế ta đc
8.f(2)=-13/4
suy ra f(2)=-13/32
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!
mình ko biết xin lỗi bạn nha!

1. Do y tỉ lệ thuận với x,ta có công thức: y = kx (k là một hằng số khác 0) (k là hệ số tỉ lệ). Thay vào,ta có: \(y=f\left(x\right)=kx=\frac{1}{2}x\)
a) Để \(f\left(x\right)=5\) hay \(y=5\) thì \(y=f\left(x\right)=\frac{1}{2}x=5\Leftrightarrow\frac{x}{2}=5\Leftrightarrow x=10\)
b) Giả sử \(x_1>x_2\Rightarrow\frac{x_1}{2}>\frac{x_2}{2}\) hay \(\frac{1}{2}.x_1>\frac{1}{2}.x_2\) hay \(f\left(x_1\right)>f\left(x_2\right)\) (đpcm)
2. Do y tỉ lệ với x,ta có công thức y = kx (k là hằng số khác 0,là hệ số tỉ lệ). Thay vào,ta có công thức: \(y=f\left(x\right)=kx=12x\)
a) Tương tự bài 1
b) Ta có: \(f\left(-x\right)=12.\left(-x\right)\)
\(-f\left(x\right)=-12.x\)
Mà \(12.\left(-x\right)=-12.x\) suy ra \(f\left(-x\right)=-f\left(x\right)\) (đpcm)

a) Với mọi \(x,y\in Q\), ta luôn luôn có:
\(x\le\left|x\right|\) và \(-x\le\left|x\right|\) ; \(y\le\left|y\right|\) và \(-y\le\left|y\right|\)
Suy ra \(x+y\le\left|x\right|+\left|y\right|\) và \(-x-y\le\left|x\right|+\left|y\right|\)
hay \(x+y\ge-\left(\left|x\right|+\left|y\right|\right)\)
Do đó \(-\left(\left|x\right|+\left|y\right|\right)\le x+y\le\left|x\right|+\left|y\right|\)
Vậy \(\left|x+y\right|\le\left|x\right|+\left|y\right|\)
b) Theo câu a ta có:
\(\left|x-y\right|+\left|y\right|\ge\left|x-y+y\right|=\left|x\right|\) ,suy ra \(\left|x-y\right|\ge\left|x\right|-\left|y\right|\)

Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.
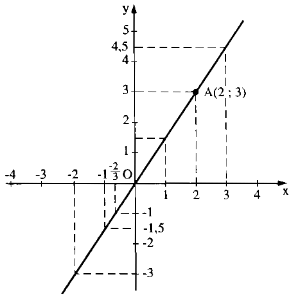
a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) =0
b)\(y=-1\Rightarrow x=\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
\(y=0\Rightarrow x=\dfrac{0}{1,5}=0\)
\(y=4,5\Rightarrow x=\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0
Đồ thị hàm số đi qua O (0; 0)
Cho x = 2 ⇒⇒ y = 1,5. 2 = 3
Ta có: A(2; 3)
Vẽ đường thẳng OA ta có đồ thị hàm số.

a) f(1) = 1,5. 1 = 1,5
f(-1) = 1,5. (-1) = -1,5
f(-2) = 1,5. (-2) = -3
f(2) = 1,5. 2 = 3
f(0) = 0
b)y=−1⇒x=\(\dfrac{-1}{1,5}=-\dfrac{2}{3}\)
b)y=0⇒x==\(\dfrac{0}{1,5}=0\)
y=4,5⇒x=\(\dfrac{4,5}{1,5}=3\)
c) y > 0 ⇒1,5x > 0 ⇒x > 0
y < 0 ⇒ 1,5x < 0 ⇒ x < 0

a, Vì hai vế đều ko âm nên ta đuợc :
\(\left|x+y\right|^2\)<=\(\left(\left|x\right|^2+\left|y\right|^2\right)\)
<=> (x+y)(x+y) <= \(\left(\left|x\right|+\left|y\right|\right)\left(\left|x\right|+\left|y\right|\right)\)
<=> \(x^2+2xy+y^2\) <= \(x^2+2\left|x\right|\left|y\right|+y^2\)
<=> xy <= |xy| ( Luôn đúng với mọi x và y )
Vậy BĐT trên đúng. Dấu ' = ' xảy ra khi x, y cùng dấu
b, Áp dụng từ câu a , bạn suy ra nhé !
a) cả 2 vế không âm nên bình phương 2 vế ta được :
\(\left|x+y\right|^2\le\left(\left|x\right|+\left|y\right|\right)^2\)
\(\Leftrightarrow\left(x+y\right)\left(x+y\right)\le\left(\left|x\right|+\left|y\right|\right).\left(\left|x\right|+\left|y\right|\right)\)
\(\Leftrightarrow x^2+2xy+y^2\le x^2+2.\left|x\right|\left|y\right|+y^2\)
\(\Leftrightarrow xy\le\left|xy\right|\) Điều này luôn đúng với mọi số x ; y .
Vậy bất đẳng thức đã cho đúng . Dầu " ="khí | xý | = xy <=> x ; y cùng dấu .
b) Áp dụng câu a) ta có : | x - y| + |y| \(\ge\) | (x-y) + y | = |x|
=> |x - y | \(\ge\)|x| + | y|
Đầu " = " xảy ra <=> (x-y) và y cùng dấu
|x + y| ≤ |x| + |y|
Với mọi x, y ∈ Q ta luôn có: x ≤ |x| và -x ≤ |x|
y ≤ |y| và -y ≤ |y|
=> x + y ≤ |x| + |y| và -x-y ≤ |x| + |y| hay x + y ≥ - (|x| + |y|)
Do đó - (|x| + |y|) ≤ x + y ≤ |x| + |y|
Vậy |x + y| ≤ |x| + |y|
Chúc bạn học tốt!!!