Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:
a + b 2 ≥ a b
Các hình chữ nhật có cùng chu vi thì a + b 2 không đổi. Từ bất đẳng thức a + b 2 ≥ a b và không đổi suy ra ab đạt giá trị lớn nhất bằng a + b 2 khi a = b.
Điều này cho thấy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Với hai số không âm a và b, bất đẳng thức Cô-si cho hai số đó là:
a + b 2 ≥ a b
Các hình chữ nhật có cùng diện tích thì ab không đổi. Từ bất đẳng thức a + b 2 ≥ a b và ab không đổi suy ra a + b 2 đạt giá trị nhỏ nhât bằng ab khi a = b.
Điều này cho thấy trong các hình chữ nhật có cùng diện tích thì hình vuông có chu vi bé nhất.

Ta có bất đẳng thức Cauchy với 2 số a,b không âm :\(\frac{a+b}{2}\ge\sqrt{ab}\)
a)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->a+b=k không đổi
->Shcn=ab\(\le\frac{\left(a+b\right)^2}{4}\)=\(\frac{k^2}{4}\)
Dấu "=" xảy ra <=>a=b<=> hình vuông
b)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->ab=k không đổi
Chu Vi HCN=2(a+b)\(\ge\)\(4\sqrt{ab}\)=4\(\sqrt{k}\)
Dấu "=" xảy ra <=> a=b <=>Hình vuông

Chu vi hình chữ nhật = 2x chiều rộng +2x chiều dài =2 cạnh hình vuông +2*
chiều dài Chu vi hình vuông = 4 cạnh hình vuông = 2 x cạnh hình vuông + 2 x cạnh hình vuông
Mà chu vi hình chữ nhật hơn chu vi hình vuông 6cm
Nên 2x chiều dài – 2 xchiều rộng = 6 2X (chiều dài – chiều rộng) = 6 Chiều dài – chiều rộng = 6:2 Chiều dài – chiều rộng = 3 cm
Diện tích hình chữ nhật hơn diện tích hình vuông bằng diện tích hình chữ nhật có cạnh 3cm, cạnh còn lại bằng chiều rộng hình chữ nhật
Chiều rộng HCN = 24:3 = 8

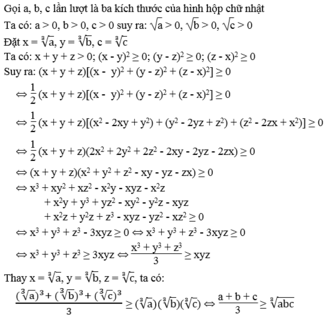
Các hình hộp chữ nhật có cùng tổng ba kích thước thì a + b + c 3 không đổi.
Vì a + b + c 3 ≥ a b c 3 và a + b + c 3 không đổi nên a b c 3 đạt giá trị lớn nhất a + b + c 3 khi a = b = c.
Vậy trong các hình hộp chữ nhật có cùng tổng ba kích thước thì hình lập phương có thể tích lớn nhất.


Gọi độ dài cạnh hình vuông là a ( a>0)
=> chu vi hình vuông là 4a
Gọi chiều dài hình chữ nhật là b, chiều dài hình chữ nhật là c ( b,c>0)
=> chu vi hình chữ nhật là: 2(c+b)
Có: chu vi hình vuông = chu vi hình chữ nhật
=> 4a=2(c+b)
<=> 2a=b+c
Áp dụng BĐT Cô-si ta có:
\(b+c\ge2.\sqrt{bc}\)
\(\Leftrightarrow2a\ge2\sqrt{bc}\)
\(\Leftrightarrow a\ge\sqrt{bc}\)
\(\Leftrightarrow a^2\ge bc\)
=> Trong tất cả các hình chữ nhật và hình vuông có cùng chu vi thì hình vuông có diện tích lớn hơn
đpcm
Tham khảo nhé~