Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a,23/99 = 23.101/99.101=2323/9999
23/99 = 23.10101/99.10101=232323/999999
b, -3737/5151=-3737.101/5151.101=-373737/515151
c, tương tự thì cứ lấy phân số đầu .2 xong rồi .4
Có: 9909/ 8808= 9/8
29727/26424= 9/8
39636/35232=9/8
Vì 9/8= 9/8= 9/8
Suy ra: 9909/8808 = 29727/26424= 39636/35232
khi rút gọn 232323/292929 và 2323/2929 thì được 23/99
Vậy ta kết luận 3 phân số trên bắng nhau
Tk đi rồi mình giải tiếp cho
Ta có:\(\dfrac{2323}{9999}=\dfrac{23.101}{99.101}=\dfrac{23}{99}\)
\(\dfrac{232323}{999999}=\dfrac{23.10101}{99.10101}=\dfrac{23}{99}\)
\(\Rightarrow\dfrac{2323}{9999}=\dfrac{232323}{999999}\)
\(\dfrac{1}{1.2.3}\) + \(\dfrac{1}{2.3.4}\) + .....+ \(\dfrac{1}{10.11.12}\)
= \(\dfrac{1}{1.2}\) - \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\) - \(\dfrac{1}{3.4}\) +....+ \(\dfrac{1}{10.11}\) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{1.2}\) + (- \(\dfrac{1}{2.3}\) + \(\dfrac{1}{2.3}\))+.......+ ( \(-\dfrac{1}{10.11}\) + \(\dfrac{1}{10.11}\)) - \(\dfrac{1}{11.12}\)
=\(\dfrac{1}{2}\) - \(\dfrac{1}{11.12}\) =\(\dfrac{1}{2}\) - \(\dfrac{1}{132}\) =\(\dfrac{66}{132}\)-\(\dfrac{1}{132}\) =\(\dfrac{65}{132}\) Vì \(\dfrac{33}{132}\) = \(\dfrac{1}{4}\) nên \(\dfrac{65}{132}\) > \(\dfrac{1}{4}\)
\(\dfrac{-5}{6}=\dfrac{-5\times4}{6\times4}=\dfrac{-20}{24}\)
\(\dfrac{3}{-8}=\dfrac{3\times\left(-3\right)}{-8\times\left(-3\right)}=\dfrac{-9}{24}\)
\(2=\dfrac{48}{24}\)
\(\dfrac{-25}{100}=\dfrac{-1}{4}=\dfrac{-1\times6}{4\times6}=\dfrac{-6}{24}\)
\(\dfrac{72}{108}=\dfrac{2}{3}=\dfrac{2\times8}{3\times8}=\dfrac{16}{24}\)
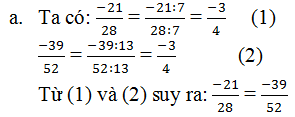
a.Ta có \(\dfrac{2323}{9999}=\dfrac{2323:101}{9999:101}=\dfrac{23}{99}\)
\(\dfrac{232323}{999999}=\dfrac{232323:10101}{999999:10101}=\dfrac{23}{99}\)
Vậy\(\dfrac{23}{99}=\dfrac{2323}{9999}=\dfrac{232323}{999999}\)(Vì cùng bằng \(\dfrac{23}{99}\))
\(\dfrac{2323}{9999}=\dfrac{2323:101}{9999:101}=\dfrac{23}{99}\)
\(\dfrac{232323}{999999}=\dfrac{232323:10101}{999999:10101}=\dfrac{23}{99}\)
cứ thế mà làm