Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: MN-NP=3cm
ΔABC=ΔMNP
=>AB=MN; BC=NP; AC=MP
MN-NP=3
=>AB-BC=3
mà AB+BC=7
nên \(AB=\dfrac{3+7}{2}=5cm;BC=AB-3=5-3=2cm\)
MP=AC
mà MP=4cm
nên AC=4cm
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=5+4+2=11\left(cm\right)\)
Chu vi tam giác MNP là:
\(C_{MNP}=MN+NP+MP=5+4+2=11\left(cm\right)\)

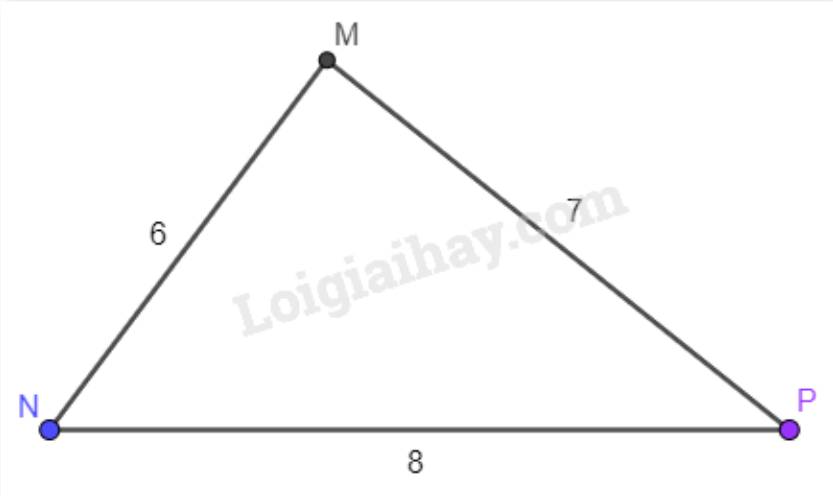
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).

Cho tam giác ABC bằng tam giác MNP. Biết AB+BC=11 cm, MN-NP= 3 cm. Khi đó MN= 7 cm.

Bài 1:
a) Ta có: MN2+MP2=152+202=625
NP2=252=625
=> MN2+MP2=NP2
=> \(\Delta MNP\)vuông tại M ( theo định lý Py-ta-go đảo)
=> đpcm
b) Ta có I là trung điểm MP
=> \(IM=IP=\frac{MP}{2}=\frac{20}{2}=10\left(cm\right)\)
Xét \(\Delta MNI\)vuông tại M có:
MN2+MI2=NI2 ( theo định lý Py-ta-go)
= 152+102=325
=> NI= \(\sqrt{325}\approx18\left(cm\right)\)
Bài 2:
Xét \(\Delta ABD\)vuông tại D có:
\(AD^2+BD^2=AB^2\)(Theo định lý Py-ta-go)
\(\Rightarrow AD^2+15^2=17^2\)
\(\Rightarrow AD^2=17^2-15^2=64=8^2\)
\(\Rightarrow AD=8\left(cm\right)\)
Lại có: AC=AD+DC
=> 17=8+DC
=> DC=9 cm
Xét \(\Delta BDC\)vuông tại D có:
\(BD^2+DC^2=BC^2\)(Theo định lý Py-ta-go)
\(\Rightarrow BC^2=15^2+9^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17\left(cm\right)\)
Vậy BC\(\approx\)17 cm

Áp dụng định lý Pitago:
\(MP^2=MN^2+NP^2 \\ \Leftrightarrow MP^2=4^2+7^2 \\ \Rightarrow MP= \sqrt{65} (cm)\)
Vậy \(MP=\sqrt{65} cm\).