Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm của BC
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
\(\Leftrightarrow\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=a\)

a) gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 2MI|= |BA|
|MI|= 1/2|BA|
=> M thuộc đường tròn tâm I, bán kính =1/2 BA
B) gọi G là trọng tâm của tam giác ABC
=> GA+ GB+ GC=0
gọi I là trung điểm của đoạn thẳng AB
=> IA+ IB=0
| 3MG|= 3/2| 2 MI|
3| MG|= 3| MI|
| MG|= | MI|
=> M thuộc đường trung trực của đoạn thẳng GI

Lời giải:
Vì $M$ là trung điểm của $BC$ nên $\overrightarrow{MB}, \overrightarrow{MC}$ là 2 vecto đối nhau.
$ABC$ là tam giác đều nên trung tuyến $AM$ đồng thời là đường cao.
$\Rightarrow \overrightarrow{MA}\perp \overrightarrow{BM}\Rightarrow \overrightarrow{MA}.\overrightarrow{MB}=0$
Khi đó ta có:
$(\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC})^2=(\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC})^2$
$=(\overrightarrow{MA}+2\overrightarrow{MB})^2$
$=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}$
$=MA^2+4MB^2$
$=AB^2+BM^2+4BM^2$
$=AB^2+5BM^2=AB^2+5(\frac{BC}{2})^2$
$=a^2+\frac{5}{4}a^2=\frac{9}{4}a^2$
$\Rightarrow |\overrightarrow{MA}+3\overrightarrow{MB}+\overrightarrow{MC}|=\frac{3}{2}a$

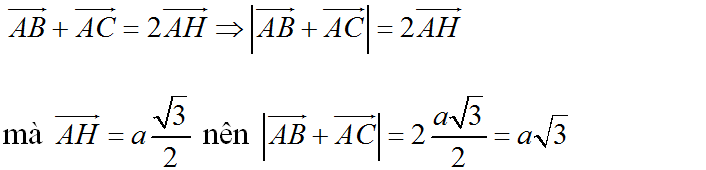
1.
Đặt \(P=\left|\overrightarrow{AD}+3\overrightarrow{AB}\right|\Rightarrow P^2=AD^2+9AB^2+6\overrightarrow{AD}.\overrightarrow{AB}\)
\(=AD^2+9AB^2=10AB^2=10a^2\)
\(\Rightarrow P=a\sqrt{10}\)
2.
Tam giác ABC đều nên AM là trung tuyến đồng thời là đường cao \(\Rightarrow AM\perp BM\)
\(AM=\dfrac{a\sqrt{3}}{2}\) ; \(BM=\dfrac{a}{2}\)
\(T=\left|\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MA}+2\overrightarrow{MB}\right|\)
\(\Rightarrow T^2=MA^2+4MB^2+4\overrightarrow{MA}.\overrightarrow{MB}=MA^2+4MB^2\)
\(=\left(\dfrac{a\sqrt{3}}{2}\right)^2+4\left(\dfrac{a}{2}\right)^2=\dfrac{7a^2}{4}\Rightarrow T=\dfrac{a\sqrt{7}}{2}\)
3.
\(T=\left|\overrightarrow{AB}+\overrightarrow{CG}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right|=\left|\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{AB}\right|\)
\(=\left|\dfrac{4}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\right|\Rightarrow T^2=\dfrac{16}{9}AB^2+\dfrac{4}{9}AC^2-\dfrac{16}{9}\overrightarrow{AB}.\overrightarrow{AC}\)
\(=\dfrac{20}{9}AB^2-\dfrac{16}{9}AB^2.cos60^0=\dfrac{20}{9}a^2-\dfrac{16}{9}a^2.\dfrac{1}{2}=\dfrac{4}{3}a^2\)
\(\Rightarrow T=\dfrac{2a}{\sqrt{3}}\)