TV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TV
1
13 tháng 7 2017
c, \(|1-3x|=\left|2x+3\right|\)
\(\Leftrightarrow\) 1-3x = 2x+ 3
\(\Leftrightarrow\)-5x = 2
\(\Leftrightarrow\) x=\(\dfrac{-2}{5}\)
Vậy x=\(\dfrac{-2}{5}\)
d, \(\left|3x-5\right|=x-2\)
ĐK: x-2 \(\ge0\Leftrightarrow x\ge2\)
TH1: 3x-5 = x-2
\(\Leftrightarrow\) 2x = 3
\(\Leftrightarrow\) x= \(\dfrac{3}{2}\left(KTM\right)\)
TH2: 3x-5 = 2- x
\(\Leftrightarrow\)4x =7
\(\Leftrightarrow\) x=\(\dfrac{7}{4}\left(KTM\right)\)
Vậy không tìm được giá trị của x thỏa mãn.
ND
19 tháng 3 2020
Bạn bạn nhân phân phối (3x-1)(x-2) và (3x-1)(7x-10)
Sau đó chuyển vế sao cho về phương trình bậc 2
Sau đó giải pt bậc hai là ra
19 tháng 3 2020
Ta có : (3x -1 ) . ( x + 2 ) = ( 3x-1 ) .( 7x - 10)
<=>3.x2 + 6x -x -2 = 21x2 -30x - 7x +10
<=> 3x2 + 5x -2 = 21x2 -37x + 10
<=> 3x2 +5x - 3 - 21x2 +37x -10 = 0
<=> -18x2 + 42x -12 = 0
<=> 3x2 -7x +2 = 0
<=> 3x2 -x -6x + 2 = 0
<=> x. ( 3x -1 ) -2.(3x -1 ) = 0
<=> (3x -1 ) . ( x - 2 ) = 0
<=> \(\orbr{\begin{cases}3x-1=0\\x-2=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}\)
Tập nghiệm của phương trình là : { \(\frac{1}{3}\); 2}
S
7 tháng 1 2019
\(\frac{\left(3x+1\right)\left(3x-2\right)}{3}+5\left(3x+1\right)=\frac{2\left(2x+1\right)\left(3x+1\right)}{3}+2\left(3x+1\right)\)
\(\Leftrightarrow\frac{2\left(2x+1\right)\left(3x+1\right)-\left(3x+1\right)\left(3x-2\right)}{3}-3\left(3x+1\right)=0\)
\(\Leftrightarrow\frac{\left(4x+2\right)\left(3x+1\right)-\left(3x+1\right)\left(3x-2\right)}{3}-3\left(3x+1\right)=0\)
\(\Leftrightarrow\frac{12x^2+10x+2-9x^2+6x-3x+2}{3}-9x-3=0\)
\(\Leftrightarrow\frac{3x^2+13x+4-27x-9}{3}=0\Leftrightarrow\frac{3x^2-14x-5}{3}=0\)
\(\Leftrightarrow3x^2-14x-5=0\Leftrightarrow3x^2-14x=5\Leftrightarrow x\left(3x-14\right)=5\)
\(.................\)
AK
7 tháng 1 2019
v: Làm tiếp nè
3x^2 - 14x - 5 = 0
<=> 3x^2 - 15x + x - 5 = 0
<=> ....
AT
19 tháng 3 2020
( 3x - 1)( x + 2) = ( 3x - 1)(7x - 10)
<=>( 3x - 1)( x + 2) - ( 3x - 1)(7x - 10) = 0
<=> ( 3x - 1)( x + 2 - 7x + 10) = 0
<=>( 3x - 1)( -6x + 12) = 0
\(\Leftrightarrow\orbr{\begin{cases}3x-1=0\\-6x+12=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}}\)
Vậy.....
19 tháng 3 2020
\(\left(3x-1\right)\left(x+2\right)=\left(3x-1\right)\left(7x-10\right)\)
\(3x^2+5x-2=21x^2-37x+10\)
\(3x^2+5x-2-21x^2+37x-10=0\)
\(-18x^2+42x-12=0\)
\(-6\left(3x-1\right)\left(x-2\right)=0\)
\(-6\ne0\)
\(\left(3x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=1\\x=2\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}}\)
13 tháng 7 2017
b) Xét khoảng \(x< 1\), pt có dạng:
\(1-x=5-3x\Leftrightarrow x=2\), không thuộc khoảng đang xét.
Xét khoảng \(1\le x\le\dfrac{5}{3}\), pt có dạng
\(x-1=5-3x\Leftrightarrow x=1,5\)
Phương trình nghiệm đúng với mọi x thuộc khoảng đang xét.
Xét khoảng \(x>\dfrac{5}{3}\), pt có dạng
\(x-1=3x-5\Leftrightarrow x=2\)
14 tháng 7 2017
Xét khoảng x<1, pt có dạng:
-2x+[-(x+1]=2 <=> x=-1
Nhận nghiệm vì nghiệm thuộc khoảng đang xét.
Xét khoảng \(-1\le x\le0\), pt có dạng:
2x-[-(x+1)]=2 <=> x=1/3
Loại nghiệm vì không thuộc khoảng đang xét
Xét khoảng x>0, pt có dạng:
2x-(x+1)=2 <=> x=3
Nhận nghiệm vì thuộc khoảng đang xét
S={-1;3}
21 tháng 3 2021
a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3
30 tháng 1 2018
a) \(2x^3 + 6x^2 = x^2 +3x\)
\(\Leftrightarrow2x^2\left(x+3\right)=x\left(x+3\right)\)
\(\Leftrightarrow2x^2\left(x+3\right)-x\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(2x^2-x\right)=0\)
\(\Leftrightarrow\left(x+3\right).x\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
S = \(\left\{-3;0;\dfrac{1}{2}\right\}\)
b) \((3x-1) (x^2 +2 ) = (3x-1) (7x - 10)\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2\right)-\left(3x-1\right)\left(7x-10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-7x+12\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=3\\x=4\end{matrix}\right.\)
S = \(\left\{\dfrac{1}{3};3;4\right\}\)
Q
23 tháng 6 2017
a) \(2\left|x\right|-\left|x+1\right|=2\) (1)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\left(x+1\right)=2\left(đk:x\ge0;x+1\ge0\right)\\2\cdot\left(-x\right)-\left(x+1\right)=2\left(đk:x< 0;x+1\ge0\right)\\2x-\left(-\left(x+1\right)\right)=2\left(đk:x\ge0;x+1< 0\right)\\2\cdot\left(-x\right)-\left(-\left(x+1\right)\right)=2\left(đk:x< 0:x+1< 0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(đk:x\ge0;x\ge-1\right)\\x=-1\left(đk:x< 0;x\ge-1\right)\\x=\dfrac{1}{3}\left(đk:x\ge0;đk:x< -1\right)\\x=-1\left(đk:x< 0;x< -1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x\in\varnothing\\x\in\varnothing\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{-1;3\right\}\)
- làm tương tự
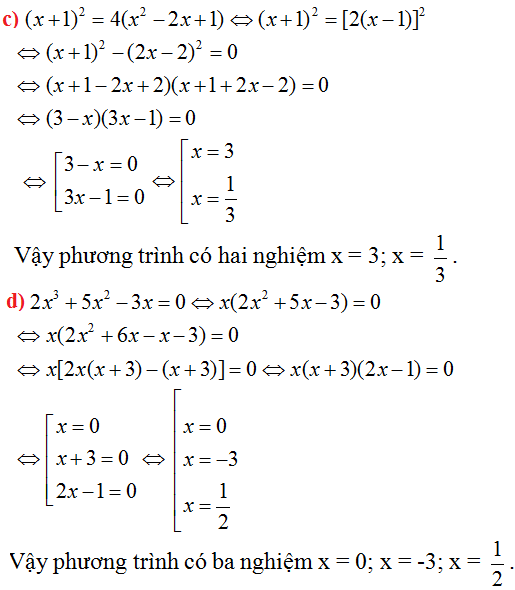
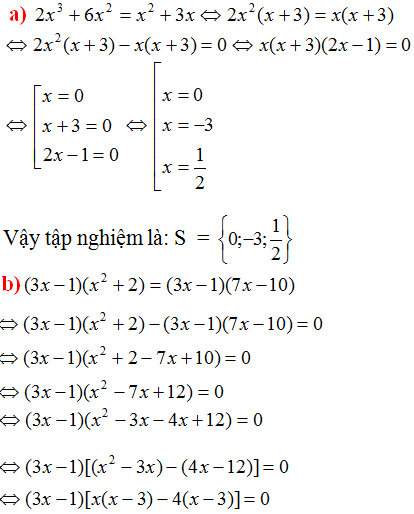
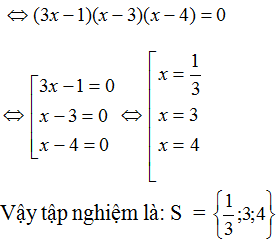
\(\left|3x-1\right|=1-3x\)
+) Xét \(x\ge\dfrac{1}{3}\) có:
\(3x-1=1-3x\Leftrightarrow6x=2\Leftrightarrow x=\dfrac{1}{3}\) ( t/m )
+) Xét \(x< \dfrac{1}{3}\) có:
\(1-3x=1-3x\)
\(\Leftrightarrow x\in R\forall x< \dfrac{1}{3}\)
Vậy \(x\le\dfrac{1}{3}\)