123457757=37568274×er=hm÷er=?

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TT

Trần Thanh Vân

26 tháng 5 2021 - olm

123457757=37568274×er=hm÷er=?

#Toán lớp 12

1

TT

Trần Thanh Vân

26 tháng 5 2021

Hỏi gi là rẻ rồi thì hm sẽ là wh

Các câu hỏi dưới đây có thể giống với câu hỏi trên

KA

Kim Anh Dư

8 tháng 5 2018

Cho tam giác ABC vuông tại A, đường cao AH. Gọi M là hình chiếu của H lên AB,N là trung điểm của AC, P là giao điểm của AH và CM.

a, chứng minh tam giác ABC đồng dạng với tam giác HAC

b, chứng minh AH. AH=AC. HM

C, chứng minh B, P, N thẳng hàng

#Toán lớp 12

0

QN

Quỳnh Như

31 tháng 3 2019

Bài 1: Cho ABC vuông tại A có . Trên cạnh BC lấy điểm D sao cho BA = BD. Tia phân giác của cắt AC tại I a/ Chứng minh BAD đều b/ Chứng minh IBC cân c/ Chứng minh D là trung điểm của Bc d/ ChoAB = 6cm. Tính BC, AC Bài 2 : Cho tam giác ABC vuông tại A và = 600 a) So sánh AB và AC ? b) Trên cạnh BC lấy điểm D sao cho BD = AB. Qua D dựng đường thẳng vuông góc với BC cắt tia đối tia AB tại E. Chứng minh : rABC = rDBE? c) Gọi H là...

#Toán lớp 12

0

NK

nguyễn khắc minh

28 tháng 8 2021 - olm

Giúp mình 56 tới 60 giải chi tiết với...

#Toán lớp 12

2

DN

Đặng Ngọc Quỳnh

28 tháng 8 2021

Câu 56: C

hình bạn vẽ nhé

Gọi I là trung điểm của AB

Ta có: \(CI=\frac{a\sqrt{3}}{2};SI=CI.\tan30^o=\frac{a}{2}\)

\(\Rightarrow V=\frac{1}{3}\frac{a}{2}\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{3}}{24}\)

NK

nguyễn khắc minh

28 tháng 8 2021

mọi người giúp đỡ mình với ạ

TV

Trần Việt Hoàng

18 tháng 3 2020 - olm

Thay vì giải = cách vẽ đồ thị thì câu này còn cách làm nào khác không ạ...

#Toán lớp 12

0

TH

Thiên hà

10 tháng 12 2020

Tìm các giá trị của m để hs y=X³+ (m -1)x²+xm-2 ngịch biến trên khoảng (1;3)

#Toán lớp 12

2

AM

Ami Mizuno

11 tháng 12 2020

undefined

NT

Nguyễn Thanh Thủy

4 tháng 10

m<=3

KD

Khánh Đào

18 tháng 3 2021

Hàm số \(y=\sqrt{2018x-x^2}\) nghịch biến trên khoảng nào dưới đây
A:(1010;2018)
B:(2018;\(+\infty\))
C:(0;1009)
D:(1;2018)

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

18 tháng 3 2021

ĐKXĐ: \(x\in\left[0;2018\right]\)

\(y'=\dfrac{1009-x}{\sqrt{2018x-x^2}}=0\Rightarrow x=1009\)

Hàm đồng biến trên \(\left(0;1009\right)\)

PT

Pham Trong Bach

10 tháng 9 2019

Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Diện tích xung quanh S x q của hình nón là: ...

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 9 2019

Chọn D

QN

Quỳnh Nguyễn

4 tháng 4 2019

Trong k gian Oxyz, cho M(4;1;9). Gọi (P) là mp đi qua M và cắt Ox,Oy,Oz lần luợt A,B,C (khác O) sao cho (OA+OB+OC) đạt GTNN. Tính d(I,(P)).

Mong m.n giaỉ chi tiết hộ mk với

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

6 tháng 4 2019

Gọi tọa độ các giao điểm là \(A\left(a;0;0\right)\); \(B\left(0;b;0\right)\); \(C\left(0;0;c\right)\)

Không làm mất tính tổng quát, chỉ cần xét trường hợp \(a;b;c>0\)

Phương trình mặt phẳng (P) theo đoạn chắn: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)

Ta có: \(S=OA+OB+OC=a+b+c\)

Do \(\left(P\right)\) qua M nên: \(\frac{4}{a}+\frac{1}{b}+\frac{9}{c}=1\)

Áp dụng BĐT Cauchy-Scwarz: \(\frac{2^2}{a}+\frac{1^2}{b}+\frac{3^2}{c}\ge\frac{\left(2+1+3\right)^2}{a+b+c}=\frac{36}{a+b+c}\)

\(\Rightarrow\frac{36}{a+b+c}\le1\Rightarrow a+b+c\ge36\)

\(\Rightarrow S_{min}=36\) khi \(\left\{{}\begin{matrix}a+b+c=36\\\frac{2}{a}=\frac{1}{b}=\frac{3}{c}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=12\\b=6\\c=18\end{matrix}\right.\)

Phương trình (P) khi đó có dạng: \(\frac{x}{12}+\frac{y}{6}+\frac{z}{18}=1\)

Hay chuyển dạng chính tắc: \(3x+6y+2z-36=0\)

Không thấy điểm I ở đâu để tính tiếp cả, nhưng đến đây thì mọi chuyện đơn giản, chỉ cần áp dụng công thức khoảng cách vào là xong.

PT

Pham Trong Bach

20 tháng 6 2018

Khối hai mươi mặt đều thuộc loại nào sau đây?

A. 3 ; 4

B. 4 ; 3

C. 3 ; 5

D. 5 ; 3

#Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 6 2018

Chọn C

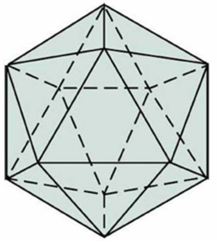
Khối hai mươi mặt đều có các mặt là tam giác nên thuộc loại 3 ; 5 .

ST

Shyn Trương

15 tháng 4 2021

#Toán lớp 12

1

TN

Trung Nguyen

15 tháng 4 2021

Gọi A là điểm biểu diễn số phức z

Khi đó A nằm trên đường trung trực của đoạn thẳng đi qua hai điểm (0;2) và (2;4). Ta tìm được pt đường thẳng đó là: d: x+y-4=0

|z|=OA min khi và chỉ khi A là hình chiếu của O trên d

Khi đó ta tìm được A(2;2)

->min|z|=\(2\sqrt{2}\)