
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách xác định đây là lăng trụ đứng hay xiên mà dựa vào đề cho .vd cho ltru Tam giác đều thì vẽ xiên hay đứng....


TXĐ :D=R
Ta có :\(lim_{x\rightarrow+\infty}\)=lim (-x3 +3x-1 )=+∞
\(lim_{x\rightarrow-\infty}\) =lim (-x3 +3x-1 ) =+∞
-> đồ thị hàm số ko có tiệm cận
lại có : y' =-3x2+x
y' =0 -> \(\left[\begin{array}{nghiempt}x=0\\x=\frac{1}{3}\end{array}\right.\)
bbt
| ||||

giả sử tổng của số hữu tỉ a vs số vô tỉ b là số hữu tỉ c, ta có b=c-a
mà hiệu của 2 số hữu tỉ phải là số hữu tỉ nên b là số hữu tỉ => mâu thuẫn vs giả thiết
vậy tổng của 1 số hữu tỉ với 1 số vô tỉ là 1 số vô tỉ.
VD : (6+√55) + (6-√55)=12
Có. Ví dụ: (3 - √3) và (2 + √3) là hai số vô tỉ dương, nhưng (3 - √3) + (2 + √3) = 5 là một số hữu tỉ.

Vì tam giác \(ABC\)vuông cân tại \(A\)nên \(\frac{BC}{AB}=\sqrt{2}\).
Suy ra \(\frac{PC}{PB}=\frac{PB}{PA}=\frac{BC}{AB}=\sqrt{2}\)
\(\Rightarrow\Delta PBC\)đồng dạng với \(\Delta PAB\).
\(\Rightarrow\widehat{PBC}=\widehat{PAB}\)
\(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=180^o-\widehat{PBC}-\widehat{PBA}=180^o-\widehat{ABC}=135^o\)
Dạng toán về tam giác đồng dạng nên có thể là nằm toán 8 nha bạn.

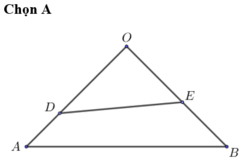
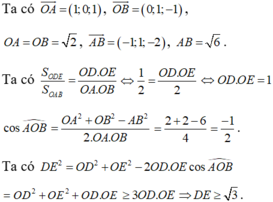
Dấu bằng xảy ra khi và chỉ khi OD = OE = 1
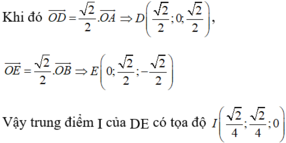
Chú ý: Sau khi chứng minh được OD=OE=1 thì ta có thể tìm trung điểm I của DE như sau:
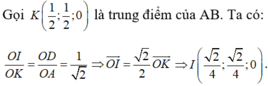

Bạn coi lại đề, chắc chắn chỗ này bạn ghi ko đúng "CM giao CN tại H"
Vì CM cắt CN tại C
 Ai Giai Dung Chinh Xac Cach Lam Va Ket Qua Dau Tien Mik Cham Cho
Ai Giai Dung Chinh Xac Cach Lam Va Ket Qua Dau Tien Mik Cham Cho
1 cộng 1 bằng 3 nha
=2
nhé bạn
HT