
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1+1=3 à
nếu sai mong bn thông cảm
~HT~
K cho mình nha cảm ơn các bn
@@@@@@@@@@@@@@@@@@@@@@@

| x + 3 | - 6x + 1 = | x + 1 |
<=> | x + 3 | - | x + 1 | - 6x + 1 = 0
Phương trình này em xét dấu và kẻ bảng rồi chia trường hợp:


hãy bình tinh vào đừng có cuống lên thì lại làm sai

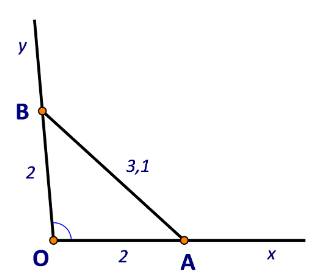
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}\cos O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{{2^2} + {2^2} - 3,{1^2}}}{{2.2.2}} \approx - 0,2\\ \Rightarrow \widehat {xOy} \approx {102^o}\end{array}\)

Dạ 2 đề là 1 ạ tại em muốn ghi lại cho mọi người hiểu ạ


Trl:
Trong toán học, một chuỗi (∑) là một tổng của một dãy các biểu thức toán học.
Trong đa số các trường hợp sử dụng, các biểu thức trong chuỗi có thể được xây dựng bằng các công thức hay thuật toán hay thậm chí bằng số ngẫu nhiên.
Chuỗi có thể hữu hạn, có số các biểu thức là hữu hạn, hay vô hạn, có số lượng các biểu thức dài vô hạn. Chuỗi hữu hạn có thể được xử lý bằng các phép tính đại số sơ cấp. Trong khi đó các chuỗi vô hạn cần các công cụ giải tích trong các ứng dụng toán học.
Trong giải tích thường phân chia chuỗi thành chuỗi số và chuỗi hàm.
Cre: Wiki
#HuyenAnh :<3
Nhớ t***
hay đấy