K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
2
CM
4 tháng 7 2019
lim x → 0 1 x 1 x + 1 − 1 = lim x → 0 1 x . − x x + 1 = lim x → 0 − 1 x + 1 = − 1.
Chọn đáp án A
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 12 2018
\(2cosx+3sinx+\dfrac{1}{3}cos2x-sin2x=\dfrac{8}{3}\)
\(\Leftrightarrow6cosx+9sinx+cos2x-3sin2x-8=0\)
\(\Leftrightarrow6cosx-6sinx.cosx+9sinx-9+1+1-2sin^2x=0\)
\(\Leftrightarrow6cosx\left(1-sinx\right)-9\left(1-sinx\right)+2\left(1-sinx\right)\left(1+sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx-9+2+2sinx=0\right)\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx+2sinx-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}1-sinx=0\\6cosx+2sinx=7\end{matrix}\right.\)
TH1: \(1-sinx=0\Rightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
TH2: \(6cosx+2sinx=7\) (1)
Do \(6^2+2^2=40< 7^2=49\Rightarrow\) pt (1) vô nghiệm
Vậy pt đã cho có nghiệm \(x=\dfrac{\pi}{2}+k2\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
a.
Chọn 1 nam từ 9 nam có 9 cách
Chọn 1 nữ từ 3 nữ có 3 cách
\(\Rightarrow\) Có \(9.3=27\) cách chọn nhóm 1 nam 1 nữ
b.
Chọn 2 nhà toán học từ 8 nahf toán học: \(C_8^2\) cách
Chọn 2 nhà vật lý từ 4 nhà vật lý: \(C_4^2\) cách
\(\Rightarrow C_8^2.C_4^2\) cách lập
c.
Các trường hợp thỏa mãn: (1 nhà toán học nữ, 2 nhà vật lý nam), (1 nhà toán học nữ, 1 nhà toán học nam, 1 nhà vật lý nam), (2 nhà toán học nữ, 1 nhà vật lý nam)
\(\Rightarrow C_3^1.C_4^2+C_3^1.C_5^1.C_4^1+C_3^2.C_4^1\) cách
M
30 tháng 8 2023
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
AH
Akai Haruma
Giáo viên
5 tháng 3 2018
Câu 1:
\(\lim _{x\to +\infty}(2x-1-\sqrt{4x^2-4x-3})=\lim_{x\to +\infty}\frac{(2x-1)^2-(4x^2-4x-3)}{2x-1+\sqrt{4x^2-4x-3}}\) (liên hợp)
\(=\lim_{x\to +\infty}\frac{4}{2x-1+\sqrt{4x^2-4x-3}}=4\lim_{x\to +\infty}\frac{1}{2x-1+\sqrt{4x^2-4x-3}}\)
Ta thấy với \(x\to +\infty\Rightarrow 2x-1+\sqrt{4x^2-4x-3}\to +\infty\)
Do đó: \(\lim_{x\to +\infty}\frac{1}{2x-1+\sqrt{4x^2-4x-3}}=0\) (theo dạng \(\lim _{t\to \infty}\frac{1}{t}=0\) )
\(\Rightarrow \lim _{x\to +\infty}(2x-1-\sqrt{4x^2-4x-3})=0\)
Câu 3:
\(\lim_{x\to 1+} (x^3-1)\sqrt{\frac{x}{x^2-1}}=\lim_{x\to 1+}(x^2+x+1)\sqrt{\frac{x(x-1)^2}{x^2-1}}\)
\(=\lim_{x\to 1+}(x^2+x+1)\sqrt{\frac{x(x-1)}{x+1}}=(1+1+1)\sqrt{\frac{1.0}{1+1}}=0\)
AH
Akai Haruma
Giáo viên
5 tháng 3 2018
Câu 2:
\(\lim_{x\to 3}\frac{\sqrt{2x^2-2}-\sqrt{4x-3}+2x-7}{9-x^2}=\lim_{x\to 3}\frac{\sqrt{2x^2-2}-4}{9-x^2}-\lim_{x\to 3}\frac{\sqrt{4x-3}-3}{9-x^2}+\lim_{x\to 3}\frac{2x-6}{9-x^2}\)
Ta có:
\(\lim_{x\to 3}\frac{2x^2-2-16}{(\sqrt{2x^2-2}+4)(9-x^2)}=\lim_{x\to 3}\frac{2(x^2-9)}{(\sqrt{2x^2-2}+4)(9-x^2)}=\lim_{x\to 3}\frac{-2}{\sqrt{2x^2-2}+4}=\frac{-1}{4}\) (1)
\(\lim_{x\to 3}\frac{\sqrt{4x-3}-3}{9-x^2}=\lim_{x\to 3}\frac{4x-3-9}{(\sqrt{4x-3}+3)(9-x^2)}=\lim_{x\to 3}\frac{4(x-3)}{(\sqrt{4x-3}+3)(9-x^2)}\)
\(=\lim_{x\to 3}\frac{-4}{(\sqrt{4x-3}+3)(3+x)}=-\frac{1}{9}\) (2)
\(\lim _{x\to 3}\frac{2x-6}{9-x^2}=\lim_{x\to 3}\frac{2(x-3)}{9-x^2}=\lim_{x\to 3}\frac{-2}{x+3}=\frac{-1}{3}\) (3)
Từ \((1); (2); (3)\Rightarrow \lim_{x\to 3}\frac{\sqrt{2x^2-2}-\sqrt{4x-3}+2x-7}{9-x^2}=\frac{-1}{4}+\frac{1}{9}-\frac{1}{3}=\frac{-17}{36}\)
PT
1
Q
4 tháng 1 2020
Cho cấp số cộng \(\left(U_n\right)\) có \(S_n=2n^2-3n\). Giá trị U1 và d là
DH
5 tháng 1 2020
Ta có: \(\frac{2n}{n^2+1}=\frac{9}{41}\Rightarrow9n^2-82n+9=0\)
\(\Rightarrow n=9\)
\(\Rightarrow\frac{9}{41}\) là số hạng thứ 9 của dãy số.
(Không chắc lắm ạ!)
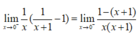
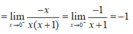
2 nha
k cho mình
hok tốt
2
Bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb