K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
28 tháng 4 2019
\(a,\frac{1}{999\cdot1000}-\frac{1}{998\cdot999}-\frac{1}{997\cdot998}-...-\frac{1}{2\cdot1}\)
\(=\frac{1}{999\cdot1000}-\left[\frac{1}{2\cdot1}+\frac{1}{2\cdot3}+...+\frac{1}{997\cdot998}+\frac{1}{998\cdot999}\right]\)
\(=\frac{1}{999\cdot1000}-\left[1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{998}-\frac{1}{999}\right]\)
\(=\frac{1}{999\cdot1000}-\left[1-\frac{1}{999}\right]=\frac{1}{999\cdot1000}-\frac{998}{999}=...\)
Tính nốt , không chắc :v
30 tháng 3 2016
Ta có:
S=1.1/2+1/2.1/3+...+1/29.1/30
=1-1/2+1/2-1/3+...+1/29-1/30
=1-1/30=29/30
29 tháng 3 2016
Có lẽ bạn viết lộn đề , dấu cuối phải là dấu nhân mới đúng/
S= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{29}-\frac{1}{30}\)
S=\(1-\frac{1}{30}\)
S=\(\frac{29}{30}\)
DT
2
DT
1
23 tháng 1 2023
Bài 2:
\(=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{999\cdot1000}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{999}-\dfrac{1}{1000}\)
=1-1/1000
=999/1000
28 tháng 3 2016
S = 1/1x1/2+1/2x1/3+1/3x1/4+...+1/28x1/29+1/29+1/30
S = 1/1-1/2+1/2-1/3+1/3-1/4+...+1/28-1/29+1/29+1/30
Đến đây ta triệt tiêu,còn lại:
S = 1/1-1/30
S = 29/30
Mình chắc chắn lun!
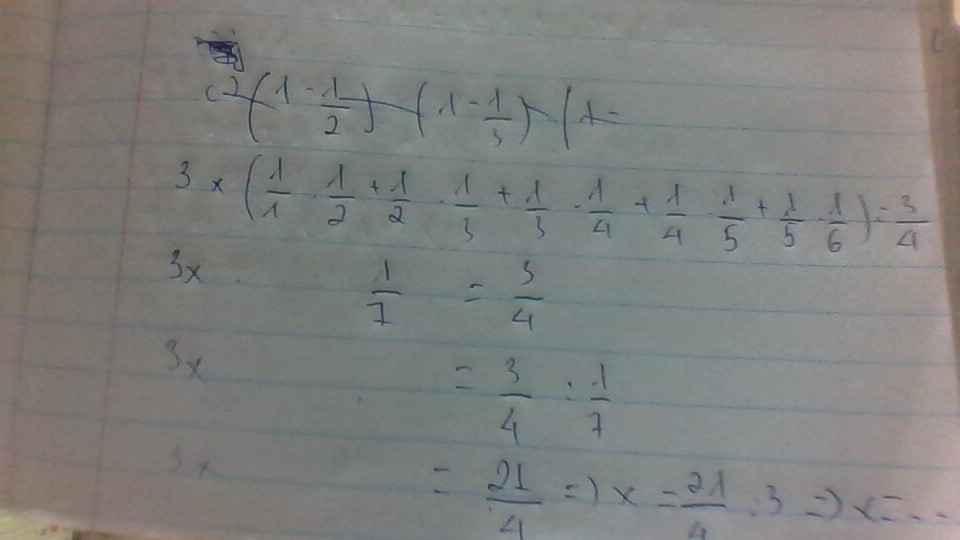
AI KẾT BN KO!
TIỆN THỂ TK MÌNH LUÔN NHA!
KONOSUBA!!!
A=\(\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{999.1000}\)\
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+.....+\frac{1}{999}-\frac{1}{1000}\)
\(A=\frac{1}{1000}-1\)
A=\(\frac{999}{1000}\)