
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
\(\lim\limits_{x\to 2-}y=\lim\limits_{x\to 2-}\frac{\sqrt{4-x^2}}{(x-2)(x-3)}=\lim\limits_{x\to 2-}\frac{\sqrt{2+x}}{\sqrt{2-x}(x-3)}=-\infty \) nên $x=2$ là TCĐ
Vì \(x\in [-2;2)\) nên không tồn tại \(\lim\limits_{x\to +\infty }y\) nên đths không có TCN
Còn $x=3$ không thể là TCĐ vì tại $x=3$ thì $\sqrt{4-x^2}$ không tồn tại .

1 + 1 = 2
Thẹc là mụt cou hỏi khó :"<
@Nghệ Mạt
#cua
 Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.
Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.

Đề bài liệu có chính xác không nhỉ? Mình chỉ có thể tìm được max bằng \(2\sqrt{2}\) (xảy ra khi \(lnx=\sqrt{2}\) và \(lny=\dfrac{1}{2}\)) và ko thể tìm được min.
À rồi OK, suy nghĩ hơi cồng kềnh 1 xíu nên hướng tìm min bị sai:
Giả thiết tương đương: \(y^{\sqrt{4-ln^2x}}=x^{1-lny}\)
\(\Rightarrow\sqrt{4-ln^2x}.lny=\left(1-lny\right)lnx\) (1)
Do \(y\ne1\Rightarrow lny\ne0\)
Nên (1) tương đương: \(\sqrt{4-ln^2x}=\left(\dfrac{1-lny}{lny}\right)lnx\) (2)
Đặt \(\left\{{}\begin{matrix}lnx=a\\lny=b\end{matrix}\right.\) thì \(log_yx=\dfrac{a}{b}\)
(2) trở thành: \(\sqrt{4-a^2}=\left(\dfrac{1-b}{b}\right)a\)
\(\Rightarrow\sqrt{4-a^2}=\dfrac{a}{b}-a\Rightarrow\dfrac{a}{b}=\sqrt{4-a^2}+a\)
Xét hàm \(f\left(a\right)=\sqrt{4-a^2}+a\) trên \(\left[-2;2\right]\)
\(f'\left(a\right)=1-\dfrac{a}{\sqrt{4-a^2}}=0\Rightarrow a=\sqrt{2}\)
\(f\left(-2\right)=-2\) ; \(f\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(a\right)_{min}=-2\) ; \(f\left(a\right)_{max}=2\sqrt{2}\)
Đáp án B

Đây là công thức bạn phải thuộc lòng, còn b là số lớn 0 và khác 1, tùy vào bài tập bạn giải sẽ có số b hợp lý.

nếu đề đúng
\(f'\left(x\right)=\frac{3}{2}x^2+m^2-4\)
\(f''\left(x\right)=3x\)
Để f(x) đạt cực đại tại x=1 <=> \(\hept{\begin{cases}f'\left(1\right)=0\\f''\left(1\right)< 0\end{cases}\Leftrightarrow}\hept{\begin{cases}\frac{3}{2}+m^2-4=0\\3.1< 0\end{cases}}\)vô lí
Vậy ko tồn tại m




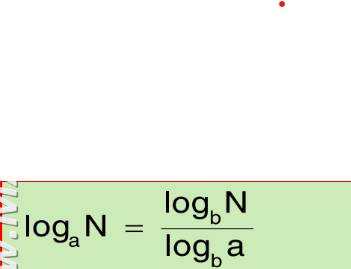

Bằng 2 nhé tớ search mạng rồi
!!!1