K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
28 tháng 12 2018
Chọn A.
[Phương pháp tự luận]
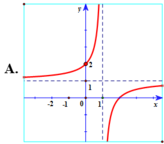
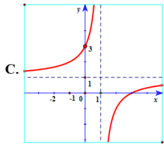
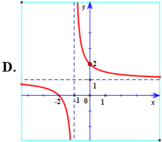
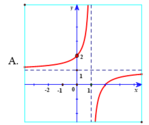
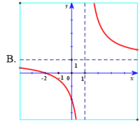
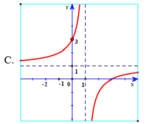
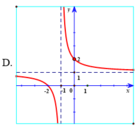
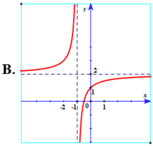
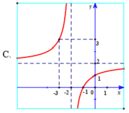
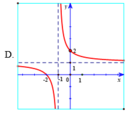
Hàm số y = x - 2 x - 1 có tiệm cận đứng x = 1 . Tiệm cận ngang y = 1 nên loại trường hợp D.
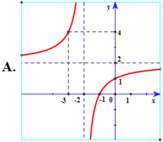
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm ( 0 ; 2 ) nên chọn đáp án A.
[Phương pháp trắc nghiệm]
d d x x - 2 x - 1 x = 10 = 1 81 > 0 suy ra hàm số y = x - 2 x - 1 đồng biến trên tập xác định, loại B, D.
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm ( 0 ; 2 ) nên chọn đáp án A.
CM
29 tháng 4 2019
Chọn A.
Hàm số y = x - 2 x - 1 có tiệm cận đứng x = 1.
Tiệm cận ngang y = 1 nên loại trường hợp D.
Đồ thị hàm số y = x - 2 x - 1 đi qua điểm (0; 2) nên chọn đáp án A.
CM
7 tháng 12 2019
Chọn C.
Ta có:
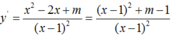
Khi đó với m > 1 thì y’ > 0, ∀x ≠ 1.
Do đó hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
NB
4
HT
27 tháng 8 2021
2114935635464+84987489= 2,115.020,622,953
99x99= 9,801
k mik nha
CM
25 tháng 5 2019
Chọn A.
[Phương pháp tự luận]
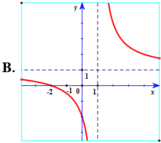
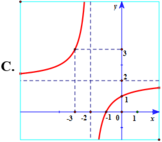
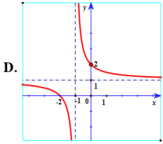
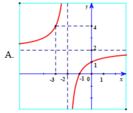
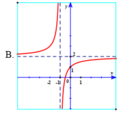
Hàm số y = 2 + 2 x 2 + x có tiệm cận đứng x = - 2 . Tiệm cận ngang y = 2 nên loại đáp án B, D.
Đồ thị hàm số y = 2 + 2 x 2 + x đi qua điểm - 3 ; 4 nên chọn đáp án A.
[Phương pháp trắc nghiệm]
d d x 2 + 2 x 2 + x x = 1 ≈ 0 , 2 > 0 suy ra hàm số y = 2 + 2 x 2 + x đồng biến trên tập xác định, loại D.
Sử dụng chức năng CALC của máy tính: C A L C → - 3 = 4 nên chọn đáp án A.
CM
22 tháng 5 2019
Chọn A.
Hàm số y = 2 + 2 x 2 + x có tiệm cận đứng x = -2.
Tiệm cận ngang y = 2 nên loại đáp án B, D.
Đồ thị hàm số y = 2 + 2 x 2 + x đi qua điểm (- 3; 4) nên chọn đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=3f'\left(x+2\right)-3\left(x^2-1\right)\)
\(y'>0\Rightarrow f'\left(x+2\right)>x^2-1\)
Đặt \(x+2=t\Rightarrow f'\left(t\right)>t^2-4t+3\)
Nhận thấy \(\left\{{}\begin{matrix}f'\left(t\right)=0\\t^2-4t+3=0\end{matrix}\right.\) đều có 2 nghiệm \(\left[{}\begin{matrix}t=1\\t=3\end{matrix}\right.\) nên ta có phác thảo 2 đồ thị:
(Và lưu ý hàm \(t^2-4t+3\) đồng biến khi t>2, nghịch biến khi t<2)
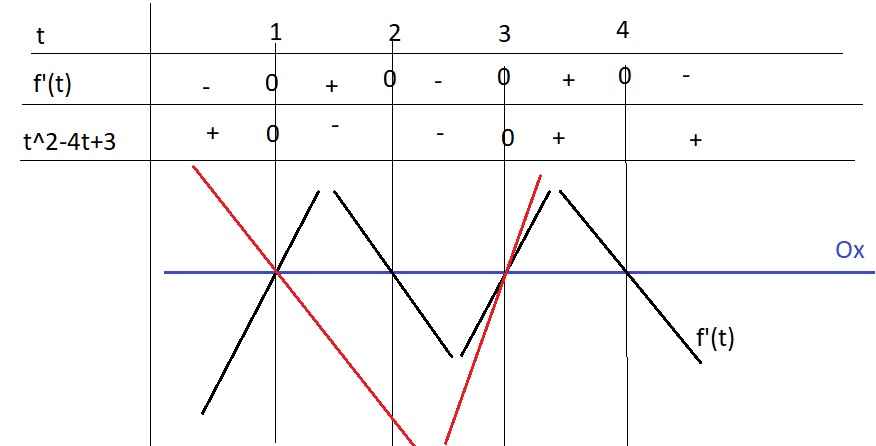
Từ đây ta thấy \(f'\left(t\right)>t^2-4t+3\) khi \(t\in\left(1;3\right)\Rightarrow x+2\in\left(1;3\right)\Rightarrow x\in\left(-1;1\right)\) và các tập con của nó
\(\Rightarrow\) B
= 2
hỏi lạ vậy?
2 nè
hỏi kì zợ