
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


cái dấu giũa số 1 và số 0 có phải là dấu nhân không
nếu là dấu nhân tì kết quả bằng 0 nha
chúc bạn học giỏi
SỐ CẦN TÌM LÀ:
1*0=0
ĐÁP SỐ :0
AI K MH MH K LẠI CHO
K CHO MH NHA

(Câu e không liên quan tới mấy câu trước, nhở)
Vẽ đường cao \(AL\). Khi đó \(AH.BC=AH\left(BL+CL\right)=AH.BL+AH.CL=2S_{AHB}+2S_{AHC}\)
Lập thêm 2 cái tương tự rồi cộng lại, phép màu sẽ xảy ra.

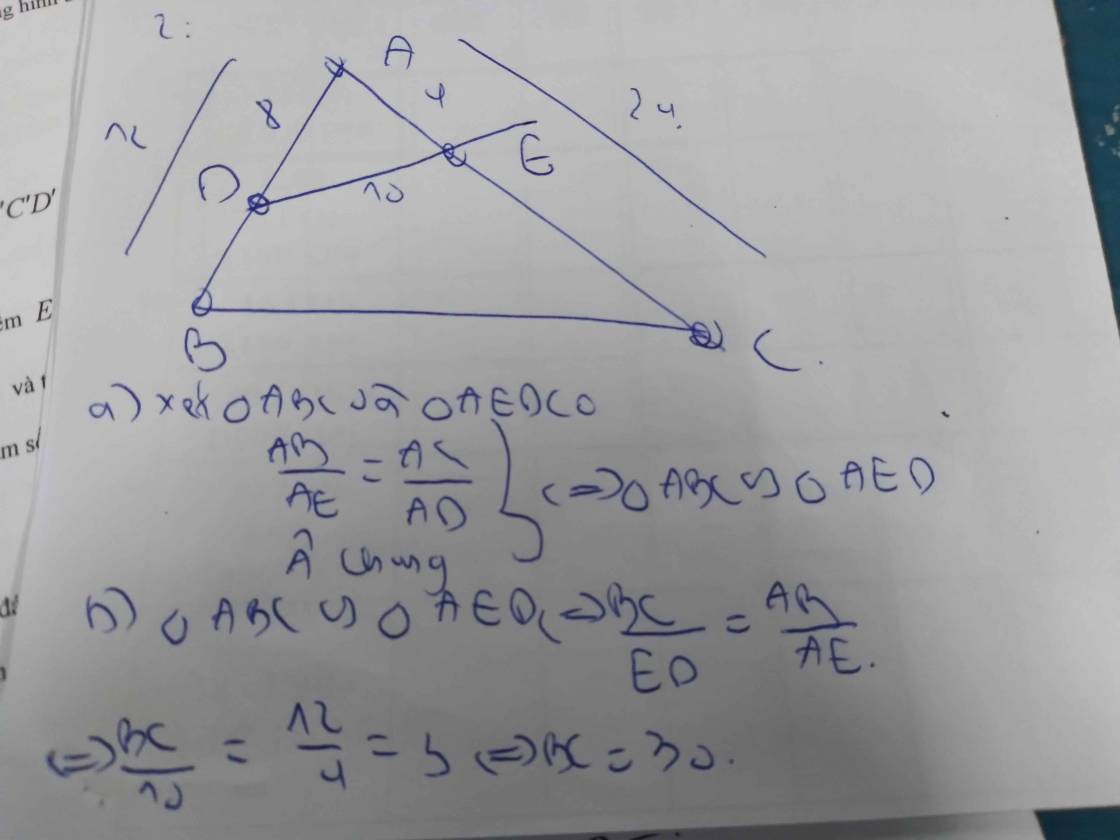
a) Ta có :
\(S_{ABC}=\dfrac{1}{2}AB.AC.sinA\)
\(S_{ADE}=\dfrac{1}{2}AD.AE.sinA\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\dfrac{AB.AC}{AD.AE}=\dfrac{48.64}{32.24}=4\)
\(\Rightarrow S_{ABC}=4S_{ADE}\)
b) Xét \(\Delta ABC\) ta có :
\(p=\left(AB+AC+BC\right):2=\left(48+36+64\right):2=74\left(cm\right)\)
Theo công thức Heron :
\(S_{ABC}=\sqrt[]{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74\left(74-48\right)\left(74-64\right)\left(74-36\right)}\)
\(\Rightarrow S_{ABC}=\sqrt[]{74.26.10.38}=4\sqrt[]{5.13.19.37}=4\sqrt[]{45695}\left(cm^2\right)\)
\(\Rightarrow S_{ADE}=\dfrac{S_{ABC}}{4}=\dfrac{4\sqrt[]{45695}}{4}=\sqrt[]{45695}\left(cm^2\right)\)
Xét \(\Delta ADE\) ta có :
Đặt \(DE=x\left(x>0\right)\)
\(p=\dfrac{\left(AD+AE+x\right)}{2}=\dfrac{\left(32+24+x\right)}{2}=\dfrac{56+x}{2}=28+\dfrac{x}{2}\left(cm\right)\)
\(S_{ADE}=\sqrt[]{p\left(p-AD\right)\left(p-AE\right)\left(p-DE\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(28+\dfrac{x}{2}-32\right)\left(28+\dfrac{x}{2}-24\right)\left(28+\dfrac{x}{2}-x\right)}\)
\(\Rightarrow S_{ADE}=\sqrt[]{\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)}\)
\(\Rightarrow S^2_{ADE}=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow45695=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\)
\(\Rightarrow5.13.19.37=\left(28+\dfrac{x}{2}\right)\left(\dfrac{x}{2}-4\right)\left(\dfrac{x}{2}+4\right)\left(28-\dfrac{x}{2}\right)\left(1\right)\)
Ta thấy khi \(x=18\) thì vế phải có :
\(\left\{{}\begin{matrix}\dfrac{x}{2}-4=5\\\dfrac{x}{2}+4=13\\28-\dfrac{x}{2}=19\\28+\dfrac{x}{2}=37\end{matrix}\right.\) \(\Rightarrow x=18\) pt (1) thỏa
Vậy \(DE=18\left(cm\right)\)

Ủa cứ tưởng bài quy luật đúng :v
\(@x=\frac{53}{24}x^4-\frac{81}{4}x^3+\frac{1651}{24}x^2-\frac{379}{4}x+46\).
Từ đó @6 = 442
Mình nghĩ đây mới là 1 lối suy nghĩ hợp lý và "thông thường" hơn chứ nhỉ, khi cho \(k\) biến và \(k\) giá trị tương ứng thì gần như luôn luôn sẽ xác định được 1 đa thức có bậc \(k-1\) tương ứng
Cho 5 giá trị biến và 5 giá trị tương ứng của hàm thì lập tức người ta sẽ nghĩ tới 1 đa thức bậc 4 dạng \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\)
Thay vào và giải hệ 5 pt 5 ẩn sẽ xác định hoàn toàn được đa thức. Nhẹ nhàng dùng 1 phép trừ giảm bớt còn 4 ẩn, sau đó ném hệ 4 ẩn vào casio và bấm là có kết quả
Trong khi quy luật của đáp án mò sấp mặt luôn @@

a) Sửa đề: C/m tứ giác BEHC nội tiếp
Xét tứ giác BEHC có
\(\widehat{BEC}=\widehat{BHC}\left(=90^0\right)\)
\(\widehat{BEC}\) và \(\widehat{BHC}\) là hai góc cùng nhìn cạnh BC
Do đó: BEHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)


1 . 0 = 0
tk mk nha mk nhanh nhất
=0 nha bạn
k cho mik nha.thanks ^_^