K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 8 2020
\(\left(\frac{15}{7}\right)^2+\left(\frac{20}{7}\right)^2=\frac{225}{49}+\frac{400}{49}=\frac{625}{49}\)
PT
1
5 tháng 7 2020
Đặt \(x^{10}=a\ge0\)
Khi đó:
\(a^{10}-10a+2029\)
\(=\left(a^{10}+1+1+1+1\right)-10a+2025\)
\(\ge5\sqrt[5]{a^{10}}-10a+2025\)
\(=5a^2-10a+2025\)
\(=5\left(a^2-2a+1\right)+2020\)
\(=5\left(a-1\right)^2+2020\ge2020\)
Đẳng thức xảy ra tại x=1 hoặc x=-1
10 tháng 7 2022
Câu 2:
a: \(=\sqrt{\left(37-35\right)\left(37+35\right)}=\sqrt{72\cdot2}=12\)
b: \(=\sqrt{\left(65-63\right)\left(65+63\right)}=\sqrt{128\cdot2}=16\)
c: \(=\sqrt{\left(221-220\right)\left(221+220\right)}=\sqrt{441}=21\)
d: \(=\sqrt{\left(117-108\right)\left(117+108\right)}=\sqrt{225\cdot9}=3\cdot15=45\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
\(A=sin^210^o+cos^220^o+sin^280^o+cos^270^o\)
\(A=\left(sin^210^o+sin^280^o\right)+\left(cos^220^o+cos^270^o\right)\)
\(A=0+0\)
\(A=0\)
17 tháng 8 2023
a: \(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2\cdot sin^270^0+1\)
b: \(=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2
18 tháng 8 2023
\(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2sin^270^0+1\)
\(B=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2
DV
2
HH
14 tháng 10 2018
Giải:
\(\sqrt{42-10\sqrt{17}}+\sqrt{33-8\sqrt{17}}\)
\(=\sqrt{\left(5-\sqrt{17}\right)^2}+\sqrt{\left(4-\sqrt{17}\right)^2}\)
\(=\left|5-\sqrt{17}\right|+\left|4-\sqrt{17}\right|\)
\(=5-\sqrt{17}+\sqrt{17}-4\)
\(=1\)
Vậy ...
15 tháng 10 2018
\(\sqrt{42-10\sqrt{17}}+\sqrt{33-8\sqrt{17}}=\sqrt{25-2.5.\sqrt{17}+17}+\sqrt{16-2.4.\sqrt{17}+17}=\sqrt{\left(5-\sqrt{17}\right)^2}+\sqrt{\left(4-\sqrt{17}\right)^2}=\left|5-\sqrt{17}\right|+\left|4-\sqrt{17}\right|=5-\sqrt{17}+\sqrt{17}-4=1\)
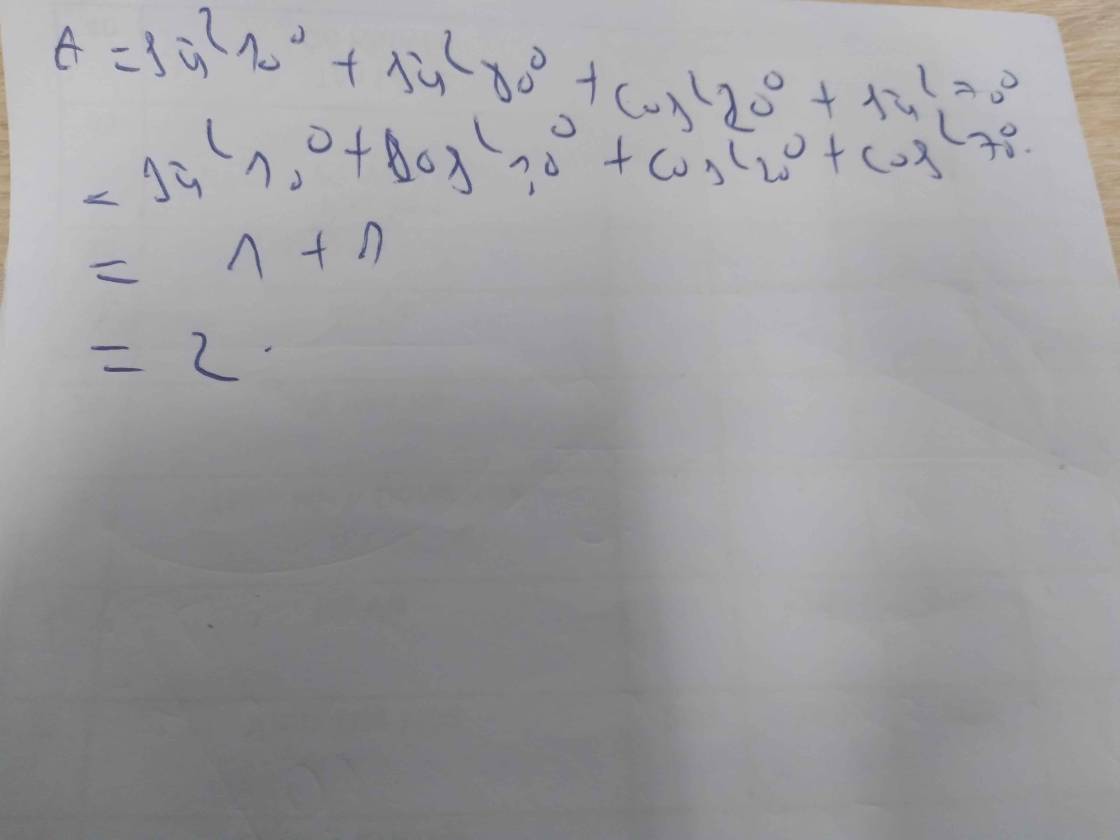
1033 = 100..00 (33 chữ số 0)