Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ tia đối của tia BC ta được tai BC', được góc ABC' kề bù với góc ABC.
Ta có ˆABC′=180∘−ˆABC=180∘−56∘=124∘ABC′^=180∘−ABC^=180∘−56∘=124∘.
b) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'. Ta được ˆC′BA=ˆABCC′BA^=ABC^ (hai góc đối đỉnh) nên ˆC′BA′=56∘.
a) Vì \(\widehat{ABC'}\) kề bù với \(\widehat{ABC}\)
\(\Rightarrow\widehat{ABC}+\widehat{ABC'}=180^o\)
mà \(\widehat{ABC}=56^o\)
\(\Rightarrow\widehat{ABC'}=124^o\)
b) Vì \(\widehat{C'BA'}\) kề bù với \(\widehat{ABC'}\)
\(\Rightarrow\widehat{C'BA'}+\widehat{ABC'}=180^o\)
mà \(\widehat{ABC'}=124^o\)
\(\Rightarrow\widehat{C'BA'}=56^o\)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

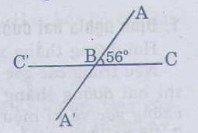
a) Trên hình vẽ bên, ta vẽ góc .
b) Vẽ tia đối của tia BC ta được tai BC', được góc ABC' kề bù với góc ABC.
Ta có .
c) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'. Ta được (hai góc đối đỉnh) nên

b, Vì ABC' kề bù với ABC
=> ABC' + ABC =180o
=> ABC' + 56o = 180o
=> ABC' = 124o
c, Vì ABC' kề bù với A'BC'
=> ABC' + A'BC' = 180o
=> 124o +A'BC' = 180o
=> A'BC' = 56o
theo mik :
a) Trên hình vẽ bên, ta vẽ góc .
b) Vẽ tia đối của tia BC ta được tai BC', được góc ABC' kề bù với góc ABC.
Ta có .
c) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'. Ta được (hai góc đối đỉnh)

Ta có hình vẽ:
\(\widehat{ABC'}\) kề bù với \(\widehat{ABC}\) nên:
\(\widehat{ABC'}+\widehat{ABC}=180^o\)
\(\widehat{ABC'}+56^o=180^o\)
\(\widehat{ABC'}=180^o-56^o=124^o\)
\(\widehat{C'BA'}\) đối đỉnh với \(\widehat{ABC}\)
nên:
\(\widehat{C'BA'}=\widehat{ABC}=56^o\)
Vậy..
b) Vẽ tia đối của tia BC ta được tai BC', được góc ABC' kề bù với góc ABC.
Ta có ˆABC′=180∘−ˆABC=180∘−56∘=124∘ABC′^=180∘−ABC^=180∘−56∘=124∘.
c) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'. Ta được ˆC′BA=ˆABCC′BA^=ABC^ (hai góc đối đỉnh) nên ˆC′BA′=56∘.