Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=-\frac{1}{4}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{NP}=\overrightarrow{NC}+\overrightarrow{CP}=\frac{1}{3}\overrightarrow{AC}+\frac{1}{5}\overrightarrow{BC}=\frac{1}{3}\overrightarrow{AC}+\frac{1}{5}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\frac{1}{3}\overrightarrow{AC}-\frac{1}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}=-\frac{1}{5}\overrightarrow{AB}+\frac{8}{15}\overrightarrow{AC}=\frac{4}{5}\left(-\frac{1}{4}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\right)\)
\(\Rightarrow\overrightarrow{NP}=\frac{4}{5}\overrightarrow{MN}\Rightarrow M;N;P\) thẳng hàng

a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.

Có \(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}\)
\(\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{CP}\)
\(\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}\)
Cộng vế vs vế:
\(\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{BN}+\overrightarrow{CP}+\overrightarrow{AM}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}+\frac{1}{3}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}\right)\)
\(=0+\frac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=0\) (đpcm)

Hình bạn tự vẽ :
AM=AB+BM
=AB+2/3BC
=AB +2/3(BA+AC)
=AB-2/3AB+2/3C
= 1/3 AB + 2/3AC

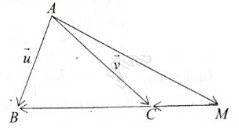
Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)
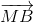 = 3
= 3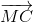 =>
=> 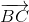 )
)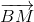 =
= 
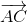 -
- 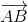 nên
nên 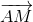 =
= 
Cách làm khác cho bài 2:
Hình vẽ: post-185288-0-41757700-1601727315.png (610×487).
Nếu \(\Delta\) // BC thì ta dễ có đpcm.
Xét trường hợp đường thẳng \(\Delta\) không song song với BC:
Gọi A' là giao điểm của \(\Delta\) và BC.
Áp dụng định lý Menelaus cho \(\Delta A'BB'\) với sự thẳng hàng của A, C, C' ta có:
\(\frac{A'C}{BC}.\frac{BA}{B'A}.\frac{B'C'}{A'C'}=1\)
\(\Rightarrow\frac{AB}{AB'}=\frac{A'C'.BC}{B'C'.A'C}\). (1)
Áp dụng định lý Menelaus cho \(\Delta A'MM'\) với sự thẳng hàng của A, C, C' ta có:
\(\frac{A'C}{MC}.\frac{MA}{M'A}.\frac{M'C'}{A'C'}=1\).
\(\Rightarrow MC=\frac{MA.M'C'.A'C}{M'A.A'C'}\). (2)
Nhân vế với vế của (1) và (2) ta được:
\(MC.\frac{AB}{AB'}=BC.\frac{MA}{MA'}.\frac{M'C'}{B'C'}\). (*)
Tương tự, \(MB.\frac{AC}{AC'}=BC.\frac{MA}{MA'}.\frac{M'B'}{B'C'}\). (**)
Cộng vế với vế của (*) và (**) ta có đpcm.
2: Cho tam giác ABC và điểm M thuộc đoạn BC. Một đường thẳng bất kì cắt các đoạn AB, AC, AM tại các điểm B',C',M'. - Hình học - Diễn đàn Toán học