Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lời giải:
Gọi \(I(a,b,c)\) là một điểm thỏa mãn \(\overrightarrow{IA}+\overrightarrow{IB}=0\)
\(\Rightarrow (3-a,-1-b,2-c)+(1-a,-5-b,-c)=0\Rightarrow I(2,-3,1)\)
Lại có:
\(P=\overrightarrow{MA}.\overrightarrow{MB}=(\overrightarrow{MI}+\overrightarrow{IA})(\overrightarrow{MI}+\overrightarrow{IB})=MI^2+\overrightarrow{IB}.\overrightarrow{IA}\)
\(\Leftrightarrow P=MI^2-6\)
Để \(P_{\min}\Leftrightarrow MI_{\min}\), điều đó đồng nghĩa với việc \(M\) là hình chiếu của $I$ lên mặt phẳng $(P)$
Gọi \(M(a,b,c)\Rightarrow \overrightarrow{IM}=(a-2,b+3,c-1)=k(2,-1,2)\)
\(\Rightarrow \frac{a-2}{2}=\frac{b+3}{-1}=\frac{c-1}{2}\)
Mặt khác, \(2a-b+2c+9=0\) nên \(a=-2,b=-1,c=-3\)
Vậy \(M(-2,-1,-3)\)
Chọn B
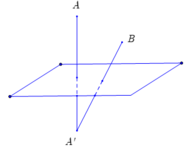
Ta có A, B cùng nằm về một phía của (P). Gọi A' đối xứng với A qua (P) suy ra A' (-2; 2; 1). Ta có MA + MB = MA' + MB ≥ BA'. Dấu bằng xảy ra khi M là giao điểm của BA' và (P). Xác định được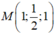 
. Suy ra Chọn B
Chọn A
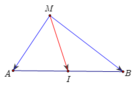
Gọi I, O lần lượt là trung điểm của AB và IC, khi đó với điểm M bất kỳ ta luôn có
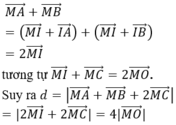
nên d nhỏ nhất khi và chỉ khi 
nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
Đường thẳng qua O (0;0;0) vuông góc với (P) có phương trình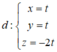 
Giao điểm của d và (P) chính là hình chiếu vuông góc M của O (0;0;0) lên mặt phẳng (P).
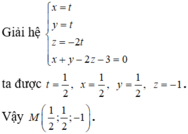
a. Do \(\left(-2\right)+1-3+1=-3< 0\)
và \(4+\left(-5\right)-6+1=-6< 0\)
nên A, B ở về cùng 1 phía của mặt phẳng (P). Do đó điểm \(C\in\left(P\right)\) sao cho \(CA+CB\) nhỏ nhất chính là giao điểm của đoạn AB với mặt phẳng (P), trong đó A' là điểm đối xứng với A qua mặt phẳng (P)
Giả sử \(A'\left(x;y;z\right)\) do A' đối xứng với A qua mặt phẳng (P) nên ta có hệ phương trình :
\(\begin{cases}\frac{x-2}{2}+\frac{y+2}{2}-\frac{zx+2}{2}+1=0\\\frac{x-2}{1}=\frac{y-1}{1}=\frac{z-3}{-1}\end{cases}\)
Giải hệ ta được \(x=0;y=3;z=1\)
Do đó \(A'\left(0;3;1\right)\)
Gọi \(C\left(x;y;z\right)\) là giao điểm của A'B với (P). Khi đó tọa độ của C' thỏa mãn phương tringf của (P) và hai vecto \(\overrightarrow{A'C};\overrightarrow{A'B}\) cùng phương. Do đó, ta có hệ phương trình :
\(\begin{cases}x+y-z+1=0\\\frac{x-0}{4-0}=\frac{y-3}{-5-3}=\frac{z-1}{6-1}\end{cases}\)
Từ phương trình thứ 2 suy ra \(y=-2x+3\) và \(z=\frac{5}{4}x+1\)
Thay vào phương trình thứ nhất ta được \(x=\frac{3}{4}\). Từ đó tìm được \(y=\frac{3}{2}\) và \(z=\frac{31}{16}\)
Vậy điềm \(C\) cần tìm là \(C\left(\frac{3}{4};\frac{3}{2};\frac{31}{16}\right)\)
b. Gọi I là trung điểm của AB. Khi đó \(I\left(1;-2;\frac{9}{2}\right)\) và với mọi điểm D đều có \(\overrightarrow{DA}+\overrightarrow{DB}=2\overrightarrow{DI}\)
Vậy \(D\in\left(P\right):\left|\overrightarrow{DA}+\overrightarrow{DB}\right|\) bé nhất \(\Leftrightarrow\) D là hình chiếu của I trên mặt phẳng (P)
Gọi \(\left(x;y;z\right)\) là tọa độ của hình chiếu điểm I trên (P). Khi đó ta có hệ phương trình :
\(\begin{cases}x+y-z+1=0\\\frac{x-1}{1}=\frac{y+2}{1}=\frac{z-\frac{9}{2}}{-1}\end{cases}\)
Giải hệ ta thu được :
\(x=\frac{5}{2};y=-\frac{1}{2};z=3\)
Vậy điểm \(D\in\left(P\right)\) sao cho \(\overrightarrow{DA}+\overrightarrow{DB}\) có độ dài nhỏ nhất là \(D\left(\frac{5}{2};-\frac{1}{2};3\right)\)
Chọn C
Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
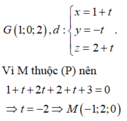
Mặt phẳng gọi là (P) đi cho dễ gõ kí tự.
Thay tọa độ A; B vào (P) cho 2 kết quả cùng dấu dương \(\Rightarrow\) A và B nằm cùng phía so với (P)
Gọi A' là điểm đối xứng với A qua (P), với điểm M bất kì thuộc (P) ta luôn có \(MA=MA'\Rightarrow MA+MB=MA'+MB\ge A'B\)
\(\Rightarrow MA+MB_{min}\) khi M;B;A' thẳng hàng hay M là giao điểm của đường thẳng A'B và (P)
Pt tham số của đường thẳng d qua A và vuông góc (P) nhận \(\left(1;-2;0\right)\) là vtcp: \(\left\{{}\begin{matrix}x=1+t\\y=-2t\\z=-2\end{matrix}\right.\)
Gọi C là giao của d và (P) \(\Rightarrow\) tọa độ C thỏa mãn:
\(1+t-2\left(-2t\right)+11=0\Rightarrow t=-\frac{12}{5}\) \(\Rightarrow C\left(-\frac{7}{5};\frac{24}{5};-2\right)\)
C là trung điểm AA' \(\Rightarrow A'\left(-\frac{19}{5};\frac{48}{5};-2\right)\)
\(\Rightarrow\overrightarrow{A'B}=\left(\frac{24}{5};-\frac{43}{5};-3\right)=\frac{1}{5}\left(24;-43;-15\right)\)
Phương trình tham số A'B: \(\left\{{}\begin{matrix}x=1+24t\\y=1-43t\\z=-5-15t\end{matrix}\right.\)
Tọa độ M thỏa mãn:
\(1+24t-2\left(1-43t\right)+11=0\Rightarrow t=-\frac{1}{11}\) \(\Rightarrow M\left(-\frac{13}{11};\frac{54}{11};-\frac{40}{11}\right)\)
Kết quả ko giống, bạn xem lại đề bài có ghi nhầm chỗ nào ko
M(7/6;2;-10/3) (Đáp án mình không trùng với 4 đáp án của bài)
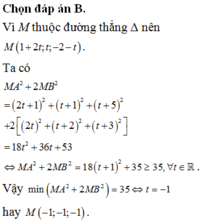
sao cho cái j có gtri nhỏ nhất v