Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Để ba số đó lập thành1 cấp số cộng thì
\(\left[{}\begin{matrix}3=2\left(2x+1+7\right)\\2x+1=2\left(3+7\right)=20\\7=2\left(2x+1+3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x+16=3\\x=\dfrac{19}{2}\\2\left(2x+4\right)=7\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{13}{4}\\x=\dfrac{19}{2}\\x=-\dfrac{1}{4}\end{matrix}\right.\)
2: Để ba số này lập thành cấp số cộng thì
\(\left[{}\begin{matrix}1=2\left(2x+1+9\right)\\2x+1=2\left(1+9\right)=20\\9=2\left(1+2x+1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x+20=1\\x=\dfrac{19}{2}\\4x+4=9\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{19}{2}\\x=-\dfrac{19}{4}\\x=\dfrac{5}{4}\end{matrix}\right.\)

5x-y;2x+1;x-y lập thành cấp số cộng nên
5x-y+x-y=2(2x+1)
=>6x-2y=4x+2
=>2x-2y=2
=>x-y=1
=>y=x-1
\(3;\sqrt{2x+y};x+1\) lập thành cấp số nhân thì \(\left(\sqrt{2x+y}\right)^2=3\left(x+1\right)\)
=>\(2x+y=3x+3\) hoặc -2x-y=3x+3
=>2x+x-1=3x+3 hoặc -2x-x+1=3x+3
=>-1=3(loại) hoặc -3x+1=3x+3
=>-6x=2
=>x=-1/3
=>y=-1/3-1=-4/3
Thử lại, ta sẽ thấy: 2x+y=-2/3-4/3=-6/3=-2<0
=>\(\sqrt{2x+y}\) không có giá trị
Vậy: Không có cặp số (x,y) nào thỏa mãn đề bài

Câu 1:
Dãy đã cho có thể viết dưới dạng công thức truy hồi sau:
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=u_n+7n\end{matrix}\right.\)
\(u_{n+1}=u_n+7n\Leftrightarrow u_{n+1}-\dfrac{7}{2}\left(n+1\right)^2+\dfrac{7}{2}\left(n+1\right)=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\)
Đặt \(v_n=u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n\Rightarrow\left\{{}\begin{matrix}v_1=1\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=v_{n-1}=...=v_1=1\)
\(\Rightarrow u_n-\dfrac{7}{2}n^2+\dfrac{7}{2}n=1\)
\(\Leftrightarrow u_n=\dfrac{7}{2}n^2-\dfrac{7}{2}n+1\)
\(\dfrac{7}{2}n^2-\dfrac{7}{2}n+1=35351\)
\(\Leftrightarrow\dfrac{7}{2}n^2-\dfrac{7}{2}n-35350=0\)
\(\Rightarrow n=101\)
Vậy đó là số hạng thứ 101
2.
Do a;b;c lập thành 1 cấp số cộng
\(\Rightarrow a+c=2b\)
\(\Leftrightarrow2R.sinA+2R.sinC=2.2R.sinB\)
\(\Leftrightarrow sinA+sinC=2sinB\)
\(\Leftrightarrow2sin\dfrac{A+C}{2}.cos\dfrac{A-C}{2}=4sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{B}{2}cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}cos\dfrac{B}{2}\)
\(\Leftrightarrow cos\dfrac{A-C}{2}=2sin\dfrac{B}{2}=2cos\dfrac{A+C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)+sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)=2cos\left(\dfrac{A}{2}\right)cos\left(\dfrac{C}{2}\right)-2sin\left(\dfrac{A}{2}\right)sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cos\left(\dfrac{A}{2}\right).cos\left(\dfrac{C}{2}\right)=3sin\left(\dfrac{A}{2}\right).sin\left(\dfrac{C}{2}\right)\)
\(\Leftrightarrow cot\left(\dfrac{A}{2}\right).cot\left(\dfrac{C}{2}\right)=3\)

1: Để ba số này lập thành 1 cấp số nhân thì
\(\left[{}\begin{matrix}\left(x+4\right)^2=\left(4x+8\right)\left(x+2\right)\\\left(x+2\right)^2=\left(x+4\right)\left(4x+8\right)\\\left(4x+8\right)^2=\left(x+2\right)\left(x+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x+4\right)^2-\left(x+4\right)^2=0\\4x^2+8x+16x+32-x^2-4x-4=0\\16x^2+64x+64-x^2-6x-8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(2x+4-x-4\right)\left(2x+4+x+4\right)=0\\3x^2+20x+28=0\\15x^2+58x+56=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x\left(3x+8\right)=0\\x\in\left\{-2;-\dfrac{14}{3}\right\}\\x\in\left\{-\dfrac{28}{15};-2\right\}\end{matrix}\right.\)
=>\(x\in\left\{0;-\dfrac{8}{3};-\dfrac{14}{3};-\dfrac{28}{15}\right\}\)
2:
Để đây là 1 cấp số nhân thì
\(\left[{}\begin{matrix}1^2=5\left(2x+4\right)\\5^2=1\cdot\left(2x+4\right)\\\left(2x+4\right)^2=1\cdot5\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}10x+20=1\\2x+4=25\\\left(2x+4\right)^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{19}{10}\\x=\dfrac{21}{2}\\2x+4=\pm\sqrt{5}\end{matrix}\right.\)
=>\(x\in\left\{-\dfrac{19}{10};\dfrac{21}{2};\dfrac{\sqrt{5}-4}{2};\dfrac{-\sqrt{5}-4}{2}\right\}\)

1, Ta có \(\left(x+4\right)^2=\left(x+2\right)\left(4x+8\right)\Leftrightarrow x^2+8x+16=4x^2+12x+16\)
\(\Leftrightarrow3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
2, tương tự

Bài 1: q=u2:u1=3:1=3
=> 3 số hạng tiếp theo: 81, 243, 729
Bài 2:
\(S_{11}=\dfrac{u_1.\left(q^{11}-1\right)}{q-1}=\dfrac{5.\left[\left(-2\right)^{11}-1\right]}{-2-1}\\ =\dfrac{5.\left(-2049\right)}{-3}=3415\)

Ta có hệ phương trình:
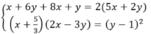
Từ đó ta suy ra
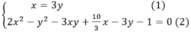
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B

1, Dãy a nha với d= 2
2,
\(u_1=3.1+1=4\\ u_2=3.2+1=7\\ d=u_2-u_1=7-4=3\)
1: Để ba số này lập thành cấp số cộng thì
\(\left[{}\begin{matrix}x-1=2\left(2x+2x-4\right)\\2x=2\left(x-1+2x-4\right)\\2x-4=2\left(x-1+2x\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}8x-8=x-1\\2x=6x-10\\2x-4=6x-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\-4x=-10\\-4x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
2: 11;15;19