Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách

Đáp án C
Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84 cách
Gọi A là biến cố:
Lấy 3 cuốn sách và không có cuốn nào là cuốn toán
Suy ra A ¯ là biến cố:
3 quyển được lấy ra có ít nhất một quyển là toán
Khi đó Ω A = C 5 3 = 10
Vậy P A = Ω A Ω = 5 42
⇒
p
A
¯
=
1
-
p
A
=
37
42

Đáp án C
Phương pháp.
Sử dụng định nghĩa của xác suất.
Lời giải chi tiết.
Tổng số sách là 4 + 3 + 2 = 9. Số cách lấy 3 quyển sách là C 9 3 = 84 (cách).
Số quyển sách không phải là sách toán là 3 + 2 = 5
Số cách lấy 3 quyển sách không phải là sách toán là C 5 3 = 10 (cách).
Do đó số cách lấy được ít nhất một quyển sách toán là 84 - 10 = 74 (cách).
Vậy xác suất để lấy đượcc ít nhất một quyển là toán là 74 84 = 37 42

Đáp án C
Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.
Lời giải:
Chọn 3 quyển sách trong 15 quyển sách có C 15 3 = 455 cách ⇒ n ( Ω ) = 455
Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.
Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:
TH1. Lấy được 2 quyển lý, 1 quyển hóa => có C 5 2 . C 6 1 = 60 cách
TH2. Lấy được 1 quyển lý, 2 quyển hóa => có C 5 1 . C 6 2 = 75 cách
TH3. Lấy được 3 quyển lý, 0 quyển hóa => có C 5 3 . C 6 0 = 10 cách
TH4. Lấy được 0 quyển lý, 3 quyển hóa => có C 5 0 . C 6 3 = 20 cách
Suy ra số phần tử của biến cố X là
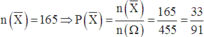
Vậy xác suất cần tính là
![]()

Đáp án A
Tổng số quyển sách trên giá là: 4 + 3 + 2 = 9 (quyển).
Số cách lấy ra 3 quyển sách từ 9 quyển sách đó là: C 9 3 .
Số cách lấy ra 3 quyển sách trong đó không có quyển sách toán nào là: C 5 3 .
Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán là C 9 3 - C 5 3 C 9 3 = 37 42

Chọn D
Tổng có 3 + 4 + 5 = 12 quyển sách được sắp xếp lên một giá sách có 3 ngăn (có 2 vách ngăn). Vì vậy, ta coi 2 vách ngăn này như 2 quyển sách giống nhau. Vậy số phần tử không gian mẫu ![]()
Gọi A là biến cố : “ Sắp xếp các 12 quyển sách lên giá sao cho không có bất kỳ hai quyển sách toán nào đứng cạnh nhau”.
+) Xếp 9 quyển sách ( lý và hóa) cùng 2 vách ngăn có 11 ! 2 ! cách
+) Lúc này, có 12 “khoảng trống” ( do 9 quyển sách ( lý và hóa) cùng 2 vách ngăn tạo ra) để xếp 3 quyển sách toán vào sao cho mỗi quyển vào một “khoảng trống” có A 12 3 cách.
Vậy có tất cả
11
!
2
!
.
A
12
3
cách. Suy ra 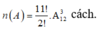
Vậy xác suất để không có bất kỳ hai quyển sách toán nào đứng cạnh nhau là:
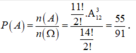

Đáp án B
30 quyển sách chia thành 15 bộ gồm :
+) 6 bộ giống nhau gồm 1 Toán- 1 Lý
+) 5 bộ giống nhau gồm 1 Lý – 1 Hóa
+) 4 bộ giống nhau gồm 1 Toán – 1 Hóa
Chọn 6 học sinh trong 15 học sinh để trao bộ Toán- Lý có C 15 6 cách
Chọn 5 học sinh trong 9 học sinh còn lại để trao bộ Lý- Hóa có C 9 5 cách
Vậy 4 học sinh còn lại sẽ được nhận bộ Toán – Hóa. Vậy có C 15 6 . C 9 5 cách trao thưởng.



\(\left(x^3+x^{-3}\right)^{18}=\sum\limits^{18}_{k=0}C^k_{18}.x^{3\left(18-k\right)}.x^{-3k}=\sum\limits^{18}_{k=0}C^k_{18}x^{54-6k}\)
Số hạng không chứa \(x\Rightarrow54-6k=0\Rightarrow k=9\)
Hệ số: \(C^9_{18}=48620\)
2/ Chọn ngẫu nhiên 7 quyển có \(C^7_{21}=116280\) cách
Các trường hợp có ít nhất 2 toán 2 lý 2 hóa: {3 toán 2 lý 2 hóa}; {2 toán 3 lý 2 hóa}; {2 toán 2 lý 3 hóa}
\(\Rightarrow\) có \(C^3_{10}.C^2_6.C^2_5+C^2_{10}.C^3_6.C^2_5+C^2_{10}.C^2_6.C^3_5=33750\) cách
Xác suất \(P=\dfrac{33750}{116280}=\dfrac{375}{1292}\)
Cách tính đúng rồi đấy, nhưng quá trình bấm máy thì bạn phải tự bấm lại cho chắc ăn