Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


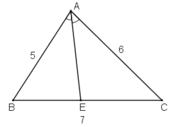
AE là đường phân giác của tam giác ABC nên
AEABAEAB = ECACECAC
Áp dụng tính chất tỉ lệ thức
AEABAEAB = ECACECAC = EB+ECAB+ACEB+ECAB+AC= BCAB+ACBCAB+AC
=> EB = AB.BCAB+ACAB.BCAB+AC = 5.75+65.75+6
EC = BC- BE ≈ 3,8

AE là phân giác BAC
=> \(\frac{EB}{EC}=\frac{AB}{AC}=\frac{5}{6}\)
=> \(\frac{EB}{5}=\frac{EC}{6}=\frac{EB+EC}{5+6}==\frac{BC}{11}=\frac{7}{11}\) ( Áp dụng dãy tỉ số bàng nhau )
=> EB = 7/11 . 5 = 35/11
=> EC = 7/11 . 6 = 42 / 11

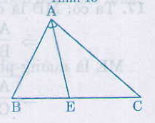
Sửa đề: BC=5,5cm
Xet ΔABC có AE là phân giác
nên EB/AB=EC/AC
=>EB/5=EC/6=(EB+EC)/(5+6)=5,5/11=0,5
=>EB=2,5cm; EC=3cm

GIẢI.
Xét tam giác ABC, có : AE tia phân giác của góc BAC (gt)
=>\(\frac{EB}{EC}=\frac{AB}{AC}\) hay \(\frac{EB}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất dãy tỉ lệ thức :
\(\frac{EB}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}=\frac{7}{11}\)
=>EB =\(\frac{5.7}{11}\) =3,18cm.
=>EC =\(\frac{6.7}{11}\) =3,82cm.
AE là đường phân giác của tam giác ABC nên
\(\frac{AE}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất tỉ lệ thức
\(\frac{AE}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}\)
\(\Rightarrow EB=\frac{AB.BC}{AB+AC}=\frac{5.7}{5+6}\)
EC = BC- BE ≈ 3,8
- See more at: http://toanhocviet.com/tinh-chat-duong-phan-giac-cua-tam-giac_n59185_g790.aspx#sthash.odDjd4Z7.dpuf