Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
b) Mẫu số chung là BCNN (5, 6) = 30. Do đó:
c) Mẫu số chung là BCNN (7, 15) = 105. Do đó:
a) −55,87−55,87
Rút gọn: −55=−1−55=−1
MC: 7
Quy đồng ta được:
−1=−77−1=−77 và 8787
b) 3,−35,−563,−35,−56
MC: 30
Thừa số phụ thứ nhất là: 30: 1 = 30
Thừa số phụ thứ hai là: 30 : 5 = 6
Thừa số phụ thứ ba là: 30 : 6 = 5
Quy đồng ta được:
3=31=3.303=903−35=(−3).65.6=−1830−56=(−5).56.5=−25303=31=3.303=903−35=(−3).65.6=−1830−56=(−5).56.5=−2530
c) −97,−1915,−1−97,−1915,−1
MC: 15. 7 = 105
Thừa số phụ thứ nhất là: 105 : 7 = 15
Thừa số phụ thứ hai là: 105 : 15 = 7
Thừa số phụ thứ ba là: 105 : 1 = 105
Quy đồng ta được:
−97=(−9).157.15=−135105−1915=(−19).715.7=−133105−1=−11=(−1).1051.105=−105105−97=(−9).157.15=−135105−1915=(−19).715.7=−133105−1=−11=(−1).1051.105=−105105

a: 2/9=4/18
1/3=6/18
5/18=5/18
b: 7/15=14/30
1/5=6/30
-5/6=-25/30
c: -21/56=-3/7
-3/16=-63/336
5/24=70/336
-21/56=-3/7=-144/336
d: \(\dfrac{-4}{7}=\dfrac{-36}{63}\)
8/9=56/63
\(-\dfrac{10}{21}=-\dfrac{30}{63}\)
e: 3/-20=-3/20=-9/60
-11/-30=11/30=22/60
7/15=28/60

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

a)\(\dfrac{-36}{63};\dfrac{56}{63};\dfrac{-30}{63}\)
b)\(\dfrac{110}{264};\dfrac{21}{264}\)

a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)

a: -9/20=-36/320
17/320=17/320
b: -7/10=-231/330
1/33=10/330
c: -5/15=-1/3=-140/420
3/20=63/420
9/70=54/420
d: 10/42=5/21=20/84
-3/28=-9/84
-55/132=-5/12=-35/84

a ,mẫu số chung nhỏ nhất là 35
b,mẫu số chung nhỏ nhất là 75
c,mẫu số chung nhỏ nhất là 24
a ,mẫu số chung nhỏ nhất là 35
b,mẫu số chung nhỏ nhất là 75
c,mẫu số chung nhỏ nhất là 24
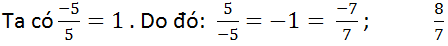
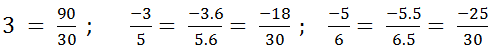
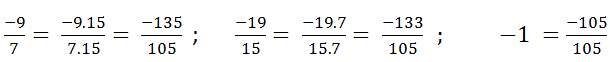


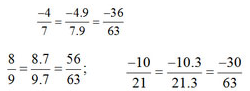
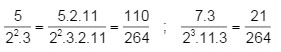
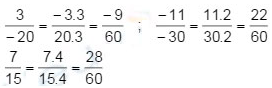
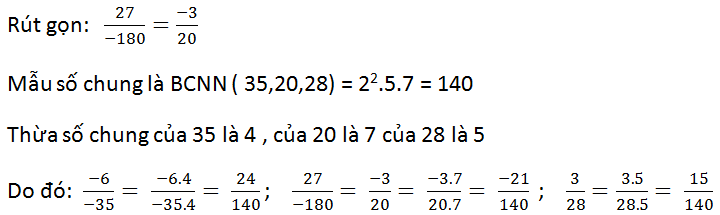
ta có : \(BCNN\left(7;21;15\right)=105\\ \dfrac{5}{7}=\dfrac{75}{105};\dfrac{-3}{21}=\dfrac{-15}{105};\dfrac{-8}{15}=\dfrac{-56}{105}\)
7 = 7; 21 = 3. 7; 15 = 3. 5
Mẫu chung: BCNN(7; 21; 15) = 3. 5. 7 = 105
Thừa số phụ: 105: 7 = 15; 105: 21 = 5; 105: 15 = 7
\(\dfrac{5}{7}=\dfrac{5.15}{7.15}=\dfrac{75}{105}\)
\(\dfrac{-3}{21}=\dfrac{-3.5}{21.5}\dfrac{-15}{105}\)
\(\dfrac{-8}{15}=\dfrac{-8.7}{15.7}=\dfrac{-56}{105}\)