Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của oto là x (km/h), x > 15 và thời gian đi từ A đến B của oto là y (h), y > 1
Vậy quãng đường AB là: xy (km)
Nếu vận tốc tăng thêm 30 km/h thì thời gian đi sẽ giảm 1 giờ. Vậy quãng đường AB là: (x + 30)(y - 1) (km)
Nếu vận tốc giảm bớt 15 km/h thì thời gian đi tăng thêm 1 giờ. Vậy quãng đường AB là: (x - 15)(y + 1)
Vậy ta có hệ phương trình:
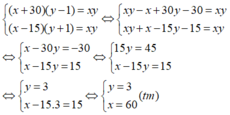
Vậy vận tốc của oto là 60 (km/h) và thời gian oto đi từ A đến B là 3 (h)

Gọi a(giờ) và b(km/h) lần lượt là thời gian và vận tốc dự định(Điều kiện: a>0; b>0)
Vì khi ô tô tăng vận tốc lên 8km/h thì đến B sớm hơn 1h nên ta có phương trình:
\(\left(a-1\right)\left(b+8\right)=ab\)
\(\Leftrightarrow ab+8a-b-8=ab\)
\(\Leftrightarrow8a-b=8\)(1)
Vì khi ô tô giảm vận tốc 4km/h thì đến B chậm hơn dự định 40 phút nên ta có phương trình:
\(\left(a+\dfrac{2}{3}\right)\left(b-4\right)=ab\)
\(\Leftrightarrow ab-4a+\dfrac{2}{3}b-\dfrac{8}{3}=ab\)
\(\Leftrightarrow-4a+\dfrac{2}{3}b=\dfrac{8}{3}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}8a-b=8\\-4a+\dfrac{2}{3}b=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8a-b=8\\-8a+\dfrac{4}{3}b=\dfrac{16}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{3}b=\dfrac{40}{3}\\8a-b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=40\\8a=8+b=48\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=40\end{matrix}\right.\)(thỏa ĐK)
Vậy: Thời gian dự định là 6 giờ
Vận tốc dự định là 40km/h

Lời giải:
Gọi vận tốc dự định là $a$ km/h
Thời gian dự định: $\frac{AB}{a}$ (giờ)
Thời gian khi tăng vận tốc 8km/h: $\frac{AB}{a+8}$ (giờ)
Thời gian khi giảm vận tốc 4km/h: $\frac{AB}{a-4}$ (giờ)
Ta có:
\(\left\{\begin{matrix}
\frac{AB}{a}-\frac{AB}{a+8}=1\\
\frac{AB}{a-4}-\frac{AB}{a}=\frac{2}{3}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
\frac{8AB}{a(a+8)}=1\\
\frac{4AB}{a(a-4)}=\frac{2}{3}\end{matrix}\right.\)
\(\Rightarrow \frac{2(a-4)}{a+8}=\frac{3}{2}\) (chia 2 pt cho nhau theo vế)
$\Rightarrow a=40$ (km/h)
$AB=\frac{a(a+8)}{8}=\frac{40.48}{8}=240$ (km)
Thời gian dự định: $\frac{AB}{a}=\frac{240}{40}=6$ (giờ)

Gọi vận tốc dự định của ô tô là x (km/h)
thời gian dự định là y (h)
Đk x > 10; y > 1
Quãng đường AB là xy (km)
Nếu vận tốc tăng thêm 20 km/h thì vận tốc xe lúc này là x + 20 km/h
Thời gian giảm 1 h ta có y-1
Ta có pt (x+20)(y-1) =xy (1)
nếu vận tốc giảm 10 km/h thì thì vận tốc xe lúc này là x-10 km/h
Thời gian tăng 1h ta có y+1
Quãng đường AB là (x-10)(y+1)
Ta có pt (x-10)(y+1) =xy (2)
Từ (1) và (2) ta có hệ pt
{(x+20)(y-1) =xy (1)
{(x-10)(y+1) =xy (2)
<=>{x-20y=-20
{x-10y=10
<=>{10y=30
{x-10y=10
<=>{y=3 (tmđk)
{x=40 (tmđk)
Vậy vận tốc dự định của ô tô là 40 km/h
Thời gian dự định là 3 giờ
Gọi vận tốc dự định của ô tô là x ( km/h ) ( x > 0 )
thời gian dự định của ô tô là y ( giờ ) ( y > 0 )
Quãng đường AB là xy
Vận tốc ô tô khi tăng thêm 20km/h là: x + 20
Thời gian ô tô đi hết quãng đường là: y - 1
\(\Rightarrow\)( x + 20 ).( y - 1 ) = xy
xy - x + 20y - 20 = xy
- x + 20y = 20 (1)
Vận tốc ô tô khi giảm đi 10km/h là: x - 10
Thời gian ô tô đi hết quãng đường là: y + 1
( x - 10 ).( y +1 ) = xy
xy + x - 10y - 10 = xy
x - 10y = 10 (2)
Từ ( 1 ) và ( 2) ta có hệ phương trình
\(\hept{\begin{cases}-x+20y=20\\x-10y=10\end{cases}\Leftrightarrow\hept{\begin{cases}x=40\\y=3\end{cases}}}\)
Vậy vận tốc dự định của ô tô là 40km/h
thời gian dự định của ô tô là 3 giờ

Gọi x ( km/h ) là vận tốc dự dịnh của ô tô và y ( giờ ) là thời gian dự định đi của ô tô . ĐK : ( x , y > 0 )
Nếu vận tốc ô tô giảm 10 km/h thì thời gian tăng 45 phút nên ta có phương trình : ( x - 10 )( y + \(\dfrac{3}{4}\)) = xy ⇔ xy + x\(\dfrac{3}{4}\) - 10y - \(\dfrac{15}{2}\) = xy
⇔ \(x\dfrac{3}{4} - 10y = \dfrac{15}{2}\) (1)
Nếu vận tốc của ô tô tăng 10 km/h thì thời gian giảm 30 phút nên ta có phương trình : ( x + 10 )( y - \(\dfrac{1}{2}\) ) = xy ⇔ - \(\dfrac{-1}{2}x\) + 10y = 5 (2)
Từ (1) và (2) ta có hpt giải ra dc x vs y

30 phút = 1/2 giờ;
45 phút = 3/4 giờ
Gọi vận tốc dự định của ô tô là x (km/h) và thời gian dự định đi của ô tô là y (giờ)
Điều kiện : x > 10; y > 1/2
Lúc đó quãng đường đi của ô tô từ A đến B là x.y (km/h)
Vì ô tô tăng vận tốc lên 10 km/h thì đến B trước 30 phút nên ta có phương trình:
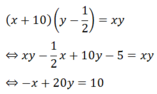
Vận tốc ô tô giảm đi 10 km/h thì đến B chậm hơn 45 phút nên ta có phương trình:
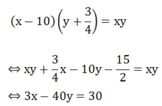
Ta có hệ phương trình
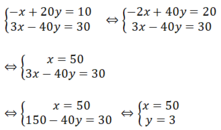
Vậy vận tốc dự định đi của ô tô là 50km/h và thời gian dự định đi của ô tô là 3 giờ.
Lời giải:
Đổi 45'=0,75h và 30'=0,5h
Gọi vận tốc ban đầu là $a$ (km/h) và thời gian đi quãng đường là $b$ (giờ)
Độ dài quãng đường AB là:
$AB=ab = (a-10)(b+0,75)=(a+10)(b-0,5)$
$\Rightarrow ab=ab+0,75a-10b-7,5=ab-0,5a+10b-5$
$\Rightarrow 0,75a-10b=7,5$ và $-0,5a+10b=5$
$\Rightarrow a=50; b=3$
Vậy vận tốc dự định là 50 km/h, thời gian dự định là 3h
Đổi 45 phút = 0,75 giờ; 30 phút = 0,5 giờ; Gọi vận tốc ban đầu, thời gian ban đầu lần lượt là: \(x\) (km/h); t (giờ); \(x\) > 0; t > 0,5
Thì vận tốc lúc tăng, thời gian đi hết quãng đường với vận tốc tăng đó lần lượt là: \({}\)\(x\) + 10 (km/h); t - 0,5 (giờ)
Và vận tốc lúc giảm; thời gian đi hết quãng đường với vận tốc giảm đó lần lượt là: \(x\) - 10 (km/h); t + 0,75 (giờ)
Do cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{x+10}{x}=\dfrac{t}{t-0,5}\left(1\right)\\\dfrac{x-10}{x}=\dfrac{t}{t+0,75}\end{matrix}\right.\) cộng vế với vế ta có: \(\dfrac{t}{t-0,5}\) + \(\dfrac{t}{t+0,75}\)= 2
⇒ 1 + \(\dfrac{0,5}{t-0,5}\)+ 1 - \(\dfrac{0,75}{t+0,75}\) = 2 ⇒\(\dfrac{0,5}{t-0,5}\)=\(\dfrac{0,75}{t+0,75}\)
⇒ 0,5.(t + 0,75) = 0,75.(t - 0,5) ⇒ 0,5t + 0,375 = 0,75t - 0,375
⇒ 0,75t - 0,5t = 0,375 + 0,375 ⇒ 0,25t = 0,75 ⇒ t = 3;
Thay t = 3 vào (1) ta có: \(\dfrac{x+10}{x}\) = \(\dfrac{3}{3-0,5}\) = 1,2
⇒ \(x\) + 10 = 1,2\(x\) ⇒ 1,2\(x\) - \(x\) = 10 ⇒ 0,2\(x\) = 10 ⇒ \(x\) = 10: 0,2 = 50
Kết luận:...