Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc ban đầu của người đó là x (km/h; \(x>5\))
Thời gian dự định là \(\dfrac{60}{x}\) (giờ)
Vận tốc lúc sau là x - 5 (km/h)
Thời gian người đó đi trên nửa quãng đường đầu là \(\dfrac{30}{x}\) (giờ)
Thời gian người đó đi trên nửa quãng đường sau là \(\dfrac{30}{x-5}\) (giờ)
Do người đó đến B chậm hơn dự định 1 giờ => ta có phương trình:
\(\dfrac{30}{x}+\dfrac{30}{x-5}=\dfrac{60}{x}+1\)
<=> \(\dfrac{30}{x-5}-\dfrac{30}{x}-1=0\)
<=> \(\dfrac{30x-30\left(x-5\right)-x\left(x-5\right)}{x\left(x-5\right)}=0\)
<=> 30x - 30x + 150 - x2 + 5x = 0
<=> x2 -5x - 150 = 0
<=> (x-15)(x+10) = 0
Mà x > 5
<=> x - 15 = 0
<=> x = 15 (tm)
KL Vận tốc dự định của người đó là 15 km/h

36 phút = \(\frac{3}{5}\)giờ
gọi x là thời gian dự định
nên quãng đường dự định (cũng là quãng đường ab) 36x
Vận tốc khi giảm 36-6=30(km/h)
nên thời gian tăng x+\(\frac{3}{5}\)
nên quãng đường thực tês (cũng là quãng đường ab) 30(x+\(\frac{3}{5}\))
vì quãng đường ab khoog dổi nên ta có phương trình sau
<=> 30(x+\(\frac{3}{5}\)) = 36x
giải pt trên ta đc x=3 nên độ dài quãng đường bằng 72

Gọi quãng đường AB là \(x\left(km\right)\left(x>0\right)\)
Thời gian người đó dự định đi là : \(\frac{x}{36}\left(km\right)\)
Thời gian người đó dự định đi là:
\(36-6=30\left(km\right)\)
Thời gian thực tế người đó đi là : \(\frac{x}{30}\left(km\right)\)
Do đến B chậm hơn dự tính \(24'=\frac{2}{5}h\) nên ta có phương trình :
\(\frac{x}{36}+\frac{2}{5}=\frac{x}{30}\)
\(\Leftrightarrow\frac{5x+36}{180}=\frac{6x}{180}\)
\(\Leftrightarrow5x+36=6x\)
\(\Leftrightarrow x=36\)
Vậy quãng đường AB là : \(36km\)
Chúc bạn học tốt !!!

Gọi quãng đường AB là x (km) (x > 0)
Thời gian người đó dự định đi là: x/36 (km)
Vận tốc đi thực tế là: 36 – 6 = 30 (km)
Thời gian thực tế người đó đi là: x/30 (km)
Do đến B chậm hơn dự tính 24’ = 2/5 h nên ta có phương trình:
⇔ 5x + 36 = 6x
⇔ x = 36
Vậy quãng đường AB là 36 km.
gọi quãng đường từ A đến B là x
thời gian dự định là t1
thời gian thực tế là t2
đổi 24 phút=2/5h
ta có
36t1=30t2
<=>36t1=30(t1+2/5)
<=>36t1=30t1+12
<=>6t1=12
<=>t1=2(h)
=> x=36.2=72
toán lớp 8 thật ak

Gọi độ dài AB là x
Thời gian dự kiến là x/12
Thời gian thực tế là 1/2+\(\dfrac{x-6}{30}\)
Theo đề, ta có: \(\dfrac{x}{12}-\dfrac{1}{2}-\dfrac{x-6}{30}=\dfrac{3}{4}\)
=>5x-30-2(x-6)=45
=>5x-30-2x+12=45
=>3x-18=45
=>3x=63
=>x=21
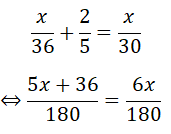
gọi độ dài quãng đường AB là \(x\) \(\left(km\right)\)\(\left(x>0\right)\)
thời gian dự định đi quãng đường AB là \(\frac{x}{15}\left(h\right)\)
thời gian thực tế đi quãng đường AB là: \(\frac{x}{15-3}=\frac{x}{12}\left(h\right)\)
theo đề bài người đó đến B chậm hơn dự tính 12 phút=1/5h nên ta có phương trình:
\(\frac{x}{12}-\frac{x}{15}=\frac{1}{5}\)
\(\Leftrightarrow\frac{5x}{60}-\frac{4x}{60}=\frac{12}{5}\)
\(\Leftrightarrow5x-4x=12\)
\(\Leftrightarrow x=12\left(TMđk\right)\)
vậy đọ dài AB là 12 km