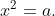Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để \(\dfrac{2}{x-1}< 0\) thì x-1<0
hay x<1
b: Để \(\dfrac{-5}{x-1}< 0\) thì x-1>0
hay x>1
c: Để \(\dfrac{7}{x-6}>0\) thì x-6>0
hay x>6
d: Để \(\dfrac{x+2}{x-6}>0\) thì x-6>0 hoặc x+2<0
=>x>6 hoặc x<-2

a) \(\left(P\Rightarrow Q\right):\)"Nếu \(x\) là một số hữu tỉ \(x^2\) cũng là một số hữu tỉ". Mệnh đề đúng.
b) Mệnh đề đảo là " Nếu \(x^2\) là một số hữu tỉ thì \(x\) là một số hữu tỉ"
c) Chẳng hạn, với \(x=\sqrt{2}\) mệnh đề này sai

a) Đúng. Mệnh đề phủ định: "1794 không chia hết cho 3".
b) Sai. "√2 không phải là một số hữu tỉ".
c) Đúng. "π không nhỏ hơn 3, 15". Dùng kí hiệu là: π ≥ 3,15 .
d) Sai. "|-125|>0".
a) Mệnh đề đúng.
Phủ định là " \(\sqrt{3}+\sqrt{2}\ne\dfrac{1}{\sqrt{3}-\sqrt{2}}\), mệnh đề này sai
b) Mệnh đề sai, vì \(\left(\sqrt{2}-\sqrt{18}\right)^2=8\).
Phủ định là " \(\left(\sqrt{2}-\sqrt{18}\right)^2\le8\)", mệnh đề này đúng
c) Mệnh đề đúng, vì \(\left(\sqrt{3}+\sqrt{12}\right)^2=27\)
Phủ định là "\(\left(\sqrt{3}+\sqrt{12}\right)^2\) là một số vô tỉ", mệnh đề này sai
d) Mệnh đề sai
Phủ định là " \(x=2\) không là nghiệm của phương trình \(\dfrac{x^2-4}{x-2}=0\)", mệnh đề này đúng

Bài 1:
a) Để x là số âm <=>x<0
<=> \(\frac{a-4}{7}< 0\Leftrightarrow a-4< 0\Leftrightarrow a< 4\)
b) Để x là số dương <=> x>0
<=> \(\frac{a-4}{7}>0\Leftrightarrow a-4>0\Leftrightarrow a>4\)
c) x k phải là số âm k phải là số dương <=>x=0
<=> \(\frac{a-4}{7}=0\Leftrightarrow a-4=0\Leftrightarrow a=4\)


1. 3 cách viết là: -0,6 ; -6/10 ; -9/15
2.Định nghĩa: Căn bậc hai của một số a không âm là số x sao cho