Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng lên, chọn mặt đất làm vật mốc
a. Ox: v0x=v=30m/s ; ax=0
Oy: v0Y=0 ; ay=-g=-10 m/s2
Ta có: x=v0X.t=30t \(\Leftrightarrow t=\dfrac{x}{30}\)
y=\(y_0+\dfrac{1}{2}at^2\)=\(y_0-\dfrac{1}{2}gt^2\) \(=80-\dfrac{1}{2}.10.\dfrac{x^2}{30^2}\)
\(\Leftrightarrow y=80-\dfrac{1}{180}x^2\)
Có : \(y=80-\dfrac{1}{2}.10.t^2\), thay y=0 ta được: t=4 (s)
Vậy thời gian kể từ lúc ném đến lúc chạm đất là 4(s)
c. Tầm xa của vật là: L=x=v0X.t=30.4=120 (m)

Qũy đạo bay của gói hàng: \(y=\dfrac{g}{2v_0^2}x^2\)
Thời gian rơi: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot490}{10}}=7\sqrt{2}s\)
Tầm bay xa: \(L=v_0t=180\cdot7\sqrt{2}=1781,91m\)
Vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(10\cdot7\sqrt{2}\right)^2+180^2}=10\sqrt{422}\)m/s

Có qua tham khảo!
a. Chọn hệ quy chiếu: gắn với mặt đất, chiều dương hướng lên, mặt đất làm mốc.
Chiếu lên Ox: \(v_{Ox}=v=30\left(\dfrac{m}{s}\right);a_X=0\)
Chiếu lên Oy: \(v_{Oy}=v_{Oy}=0;a_Y=-g=-10\left(\dfrac{m}{s^2}\right)\)
Ta có: \(x=v_{Ox}t=30t\Leftrightarrow t=\dfrac{x}{30}\)
\(y=y_o+\dfrac{1}{2}at^2=y_0-\dfrac{1}{2}gt^2=80-\dfrac{1}{2}\cdot10\cdot\dfrac{x^2}{30^2}\)
\(\Rightarrow y=80-\dfrac{1}{180}x^2\)
b. Thay y = 0 \(\Rightarrow t=4\left(s\right)\)
\(=>L=x=v_{Ox}t=30\cdot4=120\left(m\right)\)

a. Theo phương \(Ox\) có: \(x=v_0t=10t\)
Theo phương \(Oy \) có: \(y=\frac{gt^2}{2}=5t^2\)
Phương trình quỹ đạo của vật là
\(y=\frac{g}{2v_0^2}x^2=\frac{x^2}{20}\)
b. Tầm bay xa của vật là
\(L=v _0t=v_0\sqrt{\frac{2h}{g}}=10.\sqrt{\frac{2.50}{10}}=31,6\) m
c. Vận tốc của vật khi chạm đất là
\(v=\sqrt{2gh}=\sqrt{2.10.50}=31,6\) m/s

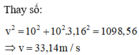


2)v0=150m/s
h =490m
g=9,8m/s2
L=?
GIẢI :
Thời gian rơi của gói hàng :
\(t=\sqrt{\frac{2.490}{9,8}}=10\left(s\right)\)
Tầm xa của gói hàng là:
\(L=v_0t=150.10=1500\left(m\right)\)
1) h =80m, v=50m/s; v0 =?
GIẢI :
Lấy g =10m/s2
Thời gian rơi là :
\(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.80}{10}}=4\left(s\right)\)
Ta có công thức : \(v=\sqrt{v_0^2+\left(gt\right)^2}=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(50=\sqrt{v_0^2+\left(10.4\right)^2}\)
=> \(v_0=30m/s\)