Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x, y (km/h) lần lượt là vận tốc của bác Toàn và cô ba Ngần đi. Điều kiện: x > 0, y > 0.
Vì hai người đi ngược chiều nhau, bác Toàn đi 1 giờ 30 phút, cô ba Ngần đi 2 giờ thì gặp nhau và tổng quãng đường họ đi được bằng khoảng cách từ làng đến thị xã nên ta có phương trình: 1,5x + 2y = 38
Quãng đường bác Toàn đi trong 1 giờ 15 phút là: 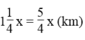
Quãng đường cô ba Ngần đi trong 1 giờ 15 phút là: ![]()
Sau 1 giờ 15 phút, hai người còn cách nhau 10,5km nên ta có phương trình:
![]()
⇔ 5x + 5y = 110
Ta có hệ phương trình:
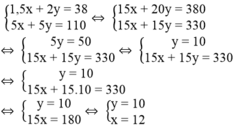
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của bác Toàn là 12km/h, vận tốc của cô ba Ngần là 10km/h.

Gọi vận tốc của xe máy là x (km/h), xe đạp y (km/h) (x,y>0)
40 phút = \(\frac{2}{3}\)giờ
Quãng đường xe máy đi là \(\frac{2}{3}\times x\)
Quãng đường xe đạp đi là \(\frac{2}{3}\times y\)
Vì họ gặp nhau nếu đi ngược chiều nên:
\(\frac{2}{3}\times x+\frac{2}{3}\times y=30\)
\(\Rightarrow x+y=45\left(1\right)\)
Nếu đi cùng chiều thì sau 2h xe máy đuổi kịp xe đạp nên ta có:
\(2x-2y=AB=30\)
\(\Rightarrow x-y=15\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\hept{\begin{cases}x+y=45\\x-y=15\end{cases}\Rightarrow\hept{\begin{cases}x=30\\y=15\end{cases}}}\)
Vậy vận tốc mỗi xe là 30 km/h và 15 km/h

Bài 1 :
Gọi vận tốc của người đi bộ là x (km/h) (x>0)
\(\Rightarrow\)vận tốc người đi xe đạp là 3x (km/h)
Vì sau 1 giờ 45 phút = \(\frac{7}{4}\)giờ thì người đi xe đạp vượt bộ hành là 21km nên quãng đường người xe đạp nhiều hơn người đi bộ 21 km.
\(\Rightarrow\frac{7}{4}.3x-\frac{7}{4}x=21\)
\(\Rightarrow3x-x=21:\frac{7}{4}\)
\(\Rightarrow2x=21.\frac{4}{7}=12\)
\(\Rightarrow x=\frac{12}{2}=6\left(km/h\right)\)
Vậy vận tốc người đi bộ và xe đạp lần lượt là 6km/h và 18km/h.
Gọi độ dài cạnh góc vuông thứ hai là \(x,48>x>4\)
=> Độ dài cạnh góc vuông thứ nhất là x−4
Vì \(\Delta\) vuông => Độ dài cạnh huyền là
\(\sqrt{x^2+\left(x-4\right)^2}=\sqrt{2x^2-8x+16}\)
Do chu vi tam giác đó là 48cm
\(\Rightarrow x+\left(x-4\right)+\sqrt{2x^2-8x+16}=48\)
\(\Rightarrow\sqrt{2x^2-8x+16}=52-2x\)
\(\Rightarrow2x^2-8x+16=\left(52-2x\right)^2\)
\(\Rightarrow2x^2-8x+16=2704-208x+4x^2\)
\(\Rightarrow-2x^2+200x-2688=0\)
\(\Rightarrow2x^2-200x+2688=0\)
\(\Rightarrow2\left(x-16\right)\left(x-84\right)=0\)
\(\Rightarrow x\in\left\{16,84\right\}\Rightarrow x=16\) vì x<48

Gọi vận tốc của người thứ nhất và người thứ hai lần lượt là x, y (km/h, x, y > 0)
Quãng đường người thứ nhất đi được khi gặp nhau là 2x (km)
Quãng đường người thứ hai đi được đến khi gặp nhau là 2y (km)
Ta có hệ phương trình
2 x + 2 y = 38 2 x − 2 y = 2 ⇔ x = 10 y = 9 (thỏa mãn)
Vậy vận tốc của người thứ nhất là 10 (km/h)
Đáp án: D

Độ dài quãng đường người thứ nhất đi từ nơi bắt đầu đến chỗ gặp nhau là:
(38+2)/2=40/2=20
Vận tốc người 1 là 20:2=10(km/h)

Câu 1:
Gọi độ dài cạnh đáy là x
=>Độ dài chiều cao là 2/5x
Theo đề, ta có: \(\dfrac{1}{2}\cdot\left(\dfrac{2}{5}x-2\right)\left(x+3\right)=\dfrac{1}{2}x\cdot\dfrac{2}{5}x-14\)
=>\(\dfrac{1}{2}\left(\dfrac{2}{5}x^2+\dfrac{6}{5}x-2x-6\right)=\dfrac{1}{5}x^2-14\)
=>1/5x^2+3/5x-x-3=1/5x^2-14
=>-2/5x=-11
=>x=11:2/5=55/2=27,5
=>Chiều cao là 11(cm)