Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(=-3xy^2z^3:\dfrac{3}{4}xyz=-3\cdot\dfrac{4}{3}\cdot\left(x:x\right)\cdot\left(y^2:y\right)\cdot\left(z^3:z\right)=-4yz^2\)
b: \(=\left(2:\dfrac{3}{4}\right)\cdot\dfrac{\left(x+y\right)^3}{\left(x+y\right)^2}=\dfrac{8}{3}\left(x+y\right)\)
c: \(=\left(x+y-z\right)^3\)

`#3107`
`a)`
`A=`\(3x^4 + \dfrac{1}3xyz - 3x^4 - \dfrac{4}3xyz + 2x^2y - 6z\)
`= (3x^4 - 3x^4) + (1/3xyz - 4/3xyz) + 2x^2y - 6z`
`= -xyz + 2x^2y - 6z`
Thay `x = 1; y = 3` và `z = 1/3` vào A
`A = -1*3*1/3 + 2*1^2*3 - 6*1/3`
`= -1 + 6 - 2`
`= 6 - 3`
`= 3`
Vậy, `A=3`
`b)`
`B=`\(4x^3 - \dfrac{2}7xyz - 4x^3 - \dfrac{4}3xyz + 4x^2y\)
`= (4x^3 - 4x^3) + (-2/7xyz - 4/3xyz) + 4x^2y`
`= -34/21 xyz + 4x^2y`
Thay `x = -1; y = 2` và `z = -1/2` vào B
`B = -34/21*(-1)*2*(-1/2) + 4*(-1)^2 * 2`
`= -34/21 + 8`
`= 134/21`
Vậy, `B = 134/21`
`c)`
`C=`\(4x^2 + \dfrac{1}2xyz - \dfrac{2}3xy^2z - 5x^2yz + \dfrac{3}4xyz\)
`= 4x^2 + (1/2xyz + 3/4xyz) - 2/3xy^2z - 5x^2yz `
`= 4x^2 + 5/4xyz - 2/3xy^2z - 5x^2yz`
Ta có:
`|y| = 2`
`=> y = +-2`
Thay `x = -1; y = 2` và `z = 1/2` vào C
`4*(-1)^2 + 5/4*(-1)*2*1/2 - 2/3*(-1)*2^2*1/2 - 5*(-1)^2*2*1/2`
`= 4 - 5/4 + 4/3 - 5`
`= -11/12`
Vậy, với `x = -1; y = 2; z = 1/2` thì `B = -11/12`
Thay `x = -1; y = -2; z = 1/2`
`B = 4*(-1)^2 + 5/4*(-1)*(-2)*1/2 - 2/3*(-1)*(-2)^2*1/2 - 5*(-1)^2*(-2)*1/2`
`= 4 + 5/4 + 4/3 + 5`
`= 139/12`
Vậy, với `x = -1; y = -2; z = 1/2` thì `B = 139/12.`

1) 2x2-8xy-5x+20y
=2x(x-4y)-5(x-4y)
=(2x-5)(x-4y)
2) x3-x2y-xy+y2
=x2(x-y)-y(x-y)
=(x2-y)(x-y)
3) x2-2xy-4z2+y2
=(x-y)2-(2z)2
=(x-y-2z)(x-y+2z)
4) a3+a2b-a2c-abc
=a2(a+b)-ac(a+b)
=(a2-ac)(a+b)
=a(a-c)(a+b)
5) x3+y3+3x2y+3xy2-x-y
=(x+y)(x2-xy+y2)+3xy(x+y)-(x+y)
=(x+y)(x2-xy+y2+3xy-1)
=(x+y)[(x+y)2-1)]
=(x+y)(x+y+1)(x+y-1)
6) x3+x2y-x2z-xyz
=x2(x+y)-xz(x+y)
=(x2-xz)(x+y)
=x(x-z)(x+y)
7) =[x(y+z)2-2xyz]+[y(z+x)2-2xyz]+z(x+y)2
=x(y2+z2)+y(z2+x2)+z(x+y)2
=xy(x+y)+z2(x+y)+z(x+y)2
=(x+y)(xy+z2+zx+zy)
=(x+y)(x+z)(y+z)
8) x3(z-y)+y3(x-z)+z3(y-x)
Tách x-z= -[z-y+y-x]

\(A=\left(x-y+z\right)^2+\left(z-y\right)^2+2\left(x-y+z\right)\left(y-z\right)=\left(x-y+z\right)\left[\left(x-y+z\right)+2\left(y-z\right)\right]+\left(z-y\right)^2=\left(x-y+z\right)\left[x+y-z\right]+\left(z-y\right)^2\)\(A=x^2-\left(y-z\right)^2+\left(z-y\right)^2=x^2\)

a: \(2x^2+3xy-14y^2\)
\(=2x^2+7xy-4xy-14y^2\)
\(=\left(2x^2+7xy\right)-\left(4xy+14y^2\right)\)
\(=x\left(2x+7y\right)-2y\left(2x+7y\right)\)
\(=\left(2x+7y\right)\left(x-2y\right)\)
b: \(\left(x-7\right)\left(x-5\right)\left(x-3\right)\left(x-1\right)+7\)
\(=\left(x-7\right)\left(x-1\right)\left(x-5\right)\left(x-3\right)+7\)
\(=\left(x^2-8x+7\right)\left(x^2-8x+15\right)+7\)
\(=\left(x^2-8x\right)^2+15\left(x^2-8x\right)+7\left(x^2-8x\right)+105+7\)
\(=\left(x^2-8x\right)^2+22\left(x^2-8x\right)+112\)
\(=\left(x^2-8x\right)^2+8\left(x^2-8x\right)+14\left(x^2-8x\right)+112\)
\(=\left(x^2-8x\right)\left(x^2-8x+8\right)+14\left(x^2-8x+8\right)\)
\(=\left(x^2-8x+8\right)\left(x^2-8x+14\right)\)
c: \(\left(x-3\right)^2+\left(x-3\right)\left(3x-1\right)-2\left(3x-1\right)^2\)
\(=\left(x-3\right)^2+2\left(x-3\right)\left(3x-1\right)-\left(x-3\right)\left(3x-1\right)-2\left(3x-1\right)^2\)
\(=\left(x-3\right)\left[\left(x-3\right)+2\left(3x-1\right)\right]-\left(3x-1\right)\left[\left(x-3\right)+2\left(3x-1\right)\right]\)
\(=\left(x-3+6x-2\right)\left(x-3-3x+1\right)\)
\(=\left(7x-5\right)\left(-2x-2\right)\)
\(=-2\left(x+1\right)\left(7x-5\right)\)
d: \(xy\left(x-y\right)+yz\left(y-z\right)+zx\left(z-x\right)\)
\(=x^2y-xy^2+y^2z-yz^2+zx\left(z-x\right)\)
\(=\left(x^2y-yz^2\right)-\left(xy^2-y^2z\right)+xz\left(z-x\right)\)
\(=y\left(x^2-z^2\right)-y^2\left(x-z\right)-xz\left(x-z\right)\)
\(=y\cdot\left(x-z\right)\left(x+z\right)-\left(x-z\right)\left(y^2+xz\right)\)
\(=\left(x-z\right)\left(xy+zy-y^2-xz\right)\)
\(=\left(x-z\right)\left[\left(xy-y^2\right)+\left(zy-zx\right)\right]\)
\(=\left(x-z\right)\left[y\cdot\left(x-y\right)-z\left(x-y\right)\right]\)
\(=\left(x-z\right)\left(x-y\right)\left(y-z\right)\)

1, 2x2 - 8xy - 5x + 20y
= (2x2 - 5x) - (8xy - 20y)
= x(2x - 5) - 4y(2x - 5)
= (2x - 5) (x - 4y)
2, x3 - x2y - xy + y2
= (x3 - xy) - (x2y - y2)
= x(x2 - y) - y(x2 - y)
= (x2 - y) (x - y)
3, x2 - 2xy - 4z2 + y2
= (x2 - 2xy + y2) - 4z2
= (x - y)2 - (2z)2
= (x - y - 2z) (x - y + 2z)
4, a3 + a2b - a2c - abc
= (a3 - a2c) + (a2b - abc)
= a2(a - c) + ab(a - c)
= (a - c) (a2 + ab)
5, x3 + y3 + 3x2y + 3xy2 - x - y
= (x3 + 3x2y + 3xy2 + y3) - (x + y)
= (x + y) 3 - (x + y)
= (x + y) [(x + y)2 - 1]
= (x + y) (x + y - 1) (x + y + 1)
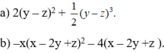
Cái nè k cần làm nhé