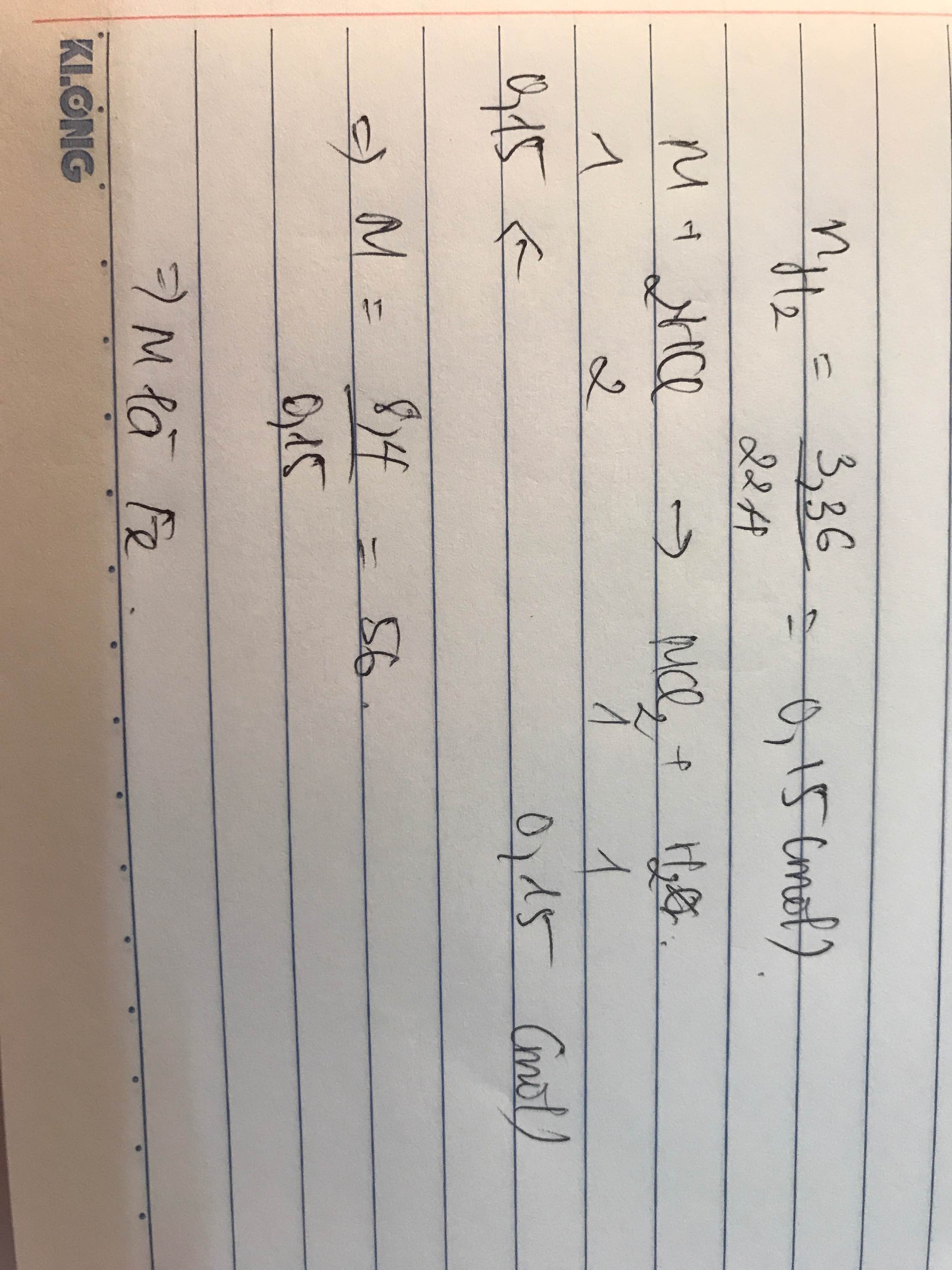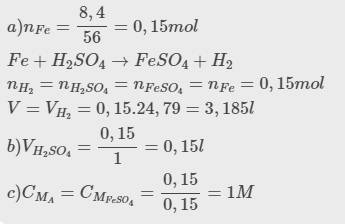Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giai: 2M + 2xH2O → 2M(OH)x + xH2
amol a mol 0,5xa mol
Theo bài ra ta có: mkim loại = Ma = 4 gam (*)
=>mdd = Ma + 96,2 – 2.0,5xa = 4 + 96,2 – xa = 100,2 – xa
Khối lượng M(OH)x = (M+17x)a = Ma + 17xa = 4 + 17xa
=>C% của M(OH)x = 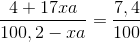
=>400 +1700xa = 741,48 – 7,4xa =>xa = 0,2 (**)
Từ (*) và (**): 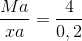
=>M = 20x
Lập bảng:
x 1 2 3
M 20 40 60
Kết luận / Ca /=>M là Ca(canxi)

4) x,y lần lượt là số mol của M và M2O3
=> nOxi=3y=nCO2=0,3 => y=0,1
Đề cho x=y=0,1 =>0,1M+0,1(2M+48)=21,6 =>M=56 => Fe và Fe2O3
=> m=0,1.56 + 0,1.2.56=16,8
2)X + 2HCl === XCl2 + H2
n_h2 = 0,4 => X = 9,6/0,4 = 24 (Mg)
=>V_HCl = 0,4.2/1 = 0,8 l

a, Ta có: \(n_{H_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
PT: \(M+H_2SO_4\rightarrow MSO_4+H_2\)
Theo PT: \(n_M=n_{H_2}=0,2\left(mol\right)\)
\(\Rightarrow M_M=\dfrac{11,2}{0,2}=56\left(g/mol\right)\)
→ M là Fe.
b, Theo PT: \(n_{FeSO_4}=n_{H_2SO_4\left(pư\right)}=n_{H_2}=0,2\left(mol\right)\)
⇒ nH2SO4 dư = 0,5.1 - 0,2 = 0,3 (mol)
\(\Rightarrow\left\{{}\begin{matrix}C_{M_{H_2SO_4\left(dư\right)}}=\dfrac{0,3}{0,5}=0,6\left(M\right)\\C_{M_{FeSO_4}}=\dfrac{0,2}{0,5}=0,4\left(M\right)\end{matrix}\right.\)
c, Ta có: \(n_{FeSO_4.7H_2O}=n_{FeSO_4}=0,2\left(mol\right)\)
\(\Rightarrow m_{FeSO_4.7H_2O}=0,2.278=55,6\left(g\right)\)