Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi số dụng cụ mỗi xưởng làm theo kế hoạch lần lượt là $a$ và $b$. Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=540\\ 1,15a+1,12b=621\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=540\\ b=0\end{matrix}\right.\) (vô lý)
Bạn xem lại đề.

- Gọi số dụng cụ xưởng 1 làm theo kế hoạch là x ( \(x\in N\), x < 360 )
- Gọi số dụng cụ xưởng 1 làm theo kế hoạch là y ( \(y\in N\), y < 360 )
Theo đề bài hai phân xưởng 1 và 2 phải làm 360 dụng cụ theo kế hoạch nên ta có phương trình : x + y = 360 ( I )
hân xưởng 1 chỉ đạt 90% kế hoạch, nhưng phân xưởng 2 lại vượt mức 10% kế hoạch nên tổng số dụng cụ cả 2 phân xưởng làm vẫn vượt 4 dụng cụ nên ta có phương trình :
\(x-10\%x+y+10\%y=360+4\left(II\right)\)
- Từ ( I ) và (II ) ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=360\\x-10\%x+y+10\%y=364\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=360\\0,9x+1,1y=364\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=360-y\\0,9\left(360-y\right)+1,1y=364\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x=360-200=160\\y=200\end{matrix}\right.\) ( TM )
Vậy số công cụ xưởng 1 làm là 160 và xưởng 2 là 200 sản phẩm .

Gọi x là sản ppham xưởng sản xuất trong 1 ngày theo kế hoạch (x>0)
=>Số ngày theo kế hoạch là :\(\frac{110}{x}\)
Số ngày thực tế là \(\frac{1100}{x+5}\)theo gia thiet cua bai toan ta co :
\(\frac{1100}{x}-\frac{1100}{x+5}=2\)
<=>1100(x+5)-1100x=2x(x+5)
<=>2x^2+10x-5500=0
<=>x=50hay x=-55 loai
Vậy theo kế hoạch mỗi ngày phân xưởng phải sản xuất là 50 sản phẩm
Gọi số sản phẩm mà phân xưởng làm trong 1 ngày là x ( x > 0 )
=> Số ngày quy định = \(\frac{1100}{x}\)( ngày )
Mỗi ngày phân xưởng sản xuất vượt mức 5 sản phẩm
=> Số ngày hoàn thành = \(\frac{1100}{x+5}\)( ngày )
Vì thế kế hoạch hoàn thành sớm hơn quy định 2 ngày
=> Ta có phương trình : \(\frac{1100}{x}-\frac{1100}{x+5}=2\)
\(\Leftrightarrow\frac{1100\left(x+5\right)}{x\left(x+5\right)}-\frac{1100\cdot x}{x\left(x+5\right)}=\frac{2x\left(x+5\right)}{x\left(x+5\right)}\)
\(\Leftrightarrow1100x+5500-1100x=2x^2+10x\)
\(\Leftrightarrow2x^2+10x-1100x-5500+1100x=0\)
\(\Leftrightarrow2x^2+10x-5500=0\)
\(\Delta'=b'^2-ac=5^2-2\cdot\left(-5500\right)=25+11000=11025\)
\(\Delta'>0\)nên phương trình đã cho có hai nghiệm phân biệt :
\(\hept{\begin{cases}x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{-5+\sqrt{11025}}{2}=50\\x_2=\frac{-b-\sqrt{\Delta'}}{a}=\frac{-5-\sqrt{11025}}{2}=-55\end{cases}}\)
x > 0 => x = 50
Vậy theo kế hoạch , mỗi ngày phân xưởng sản xuất 50 sản phẩm

Gọi số dụng cụ xí nghiệp I làm theo kế hoạch là x (dụng cụ)
Gọi số dụng cụ xí nghiệp II làm theo kế hoạch là y (dụng cụ)
Điều kiện x;y ∈ N*.
Vì theo kế hoạch hai xí nghiệp phải làm 520 dụng cụ,nên ta có phương trình: x + y = 520 (1)
Thực tế xí nghiệp I vượt mức kế hoạch 10% và xí nghiệp II vượt mức kế hoạch 12%, do đó cả 2 xí nghiệp làm đc 577 sản phẩm nên ta có phương trình:
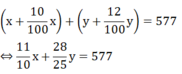
Ta có hệ phương trình
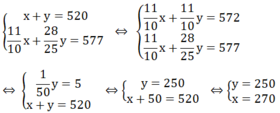
Vậy xí nghiệp I làm theo kế hoạch là 270 dụng cụ.
Xí nghiệp II làm theo kế hoạch là 250 dụng cụ.

Lời giải:
Gọi số sản phẩm làm theo kế hoạch của xưởng 1 và xưởng 2 lần lượt là $a,b$ (sp).
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=500\\ a.1,1+b.1,15=560\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=300\\ b=200\end{matrix}\right.\)
Vậy xưởng 1 và xưởng 2 theo kế hoạch phải làm lần lượt 300 sp và 200 sp.
Bài 1:
Gọi số dụng cụ phân xưởng thứ nhất phải làm là a(dụng cụ)(Điều kiện: \(a\in Z^+\))
Số dụng cụ phân xưởng thứ hai phải làm là:
300-a(dụng cụ)
Theo đề, ta có:
\(\dfrac{11}{10}a+\dfrac{6}{5}\left(300-a\right)=340\)
\(\Leftrightarrow\dfrac{11}{10}a+360-\dfrac{6}{5}a=340\)
\(\Leftrightarrow\dfrac{-1}{10}a=-20\)
hay a=200(Thỏa ĐK)
Vậy: Phân xưởng thứ nhất phải làm 200 dụng cụ
Phân xưởng thứ hai phải làm 100 dụng cụ