
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(z=1-i+i.i^2=1-i+\left(-1\right).i=1-2i\)
phần thực a=1, phần ảo b=-2
vậy chọn C

\(y=x+\dfrac{1}{x}-5\ge2\sqrt{x.\dfrac{1}{x}}-5=-3\)
Đáp án C

TXĐ: \(D=R\)
\(f'\left(x\right)=4x^3-24x\)
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\sqrt{6}\\x=-\sqrt{6}\left(loai\right)\end{matrix}\right.\)
\(\begin{matrix}f\left(0\right)=-1\\f\left(\sqrt{6}\right)=-37\\f\left(9\right)=5588\end{matrix}\)
suy ra chọn D

`2^x+8.2^{-x}<=9`
`<=>2^x+8.(2^x)^{-1}<=9`
`<=>2^x+8/(2^x)<=9`
`<=>4^x+8<=9.2^x`
`<=>(2^x)^2-9.2x^2+8<=0`
Đặt `t=2^x`
`pt<=>t^2-9t+8<=0`
`<=>(t-1)(t-8)<=0`
`<=>1<=t<=8`
`<=>1<=2^x<=8=>x in {1;2;3}`
`=>` Chọn C.3

Ta thấy : A =\(\frac{20^{10}+1}{20^{10}-1}>1\)
Ta có : A=\(\frac{20^{10}+1}{20^{10}-1}>\frac{20^{10}+1-2}{20^{10}-1-2}=\frac{20^{10}-1}{20^{10}-3}=B\)
Vậy A > B
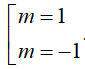
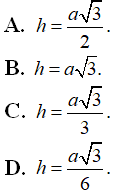
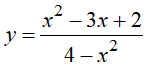 là:
là: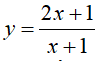 có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau
có đồ thị (C). Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ hai điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau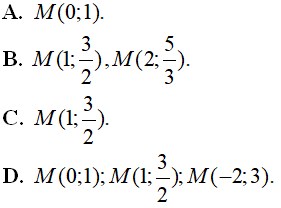 giúp mik nhe r mik tick choa pls
giúp mik nhe r mik tick choa pls
siêu easy