VL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
26 tháng 7 2018
\(A=\sqrt{\frac{5+\sqrt{21}}{5-\sqrt{21}}}+\sqrt{\frac{5-\sqrt{21}}{5+\sqrt{21}}}\)
\(=\sqrt{\frac{\left(5+\sqrt{21}\right)^2}{\left(5-\sqrt{21}\right)\left(5+\sqrt{21}\right)}}+\sqrt{\frac{\left(5-\sqrt{21}\right)^2}{\left(5-\sqrt{21}\right)\left(5+\sqrt{21}\right)}}\)
\(=\sqrt{\frac{\left(5+\sqrt{21}\right)^2}{4}}+\sqrt{\frac{\left(5-\sqrt{21}\right)^2}{4}}\)
\(=\frac{5+\sqrt{21}}{2}+\frac{5-\sqrt{21}}{2}=5\)
\(B=\sqrt{7+\sqrt{33}}+\sqrt{7-\sqrt{33}}\)
\(\Rightarrow\)\(\sqrt{2}B=\sqrt{14+2\sqrt{33}}+\sqrt{14-2\sqrt{33}}\)
\(=\sqrt{\left(\sqrt{11}+\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{11}-\sqrt{3}\right)^2}\)
\(=\sqrt{11}+\sqrt{3}+\sqrt{11}-\sqrt{3}=2\sqrt{11}\)
\(\Rightarrow\)\(B=\sqrt{22}\)
VT
7 tháng 11 2017
\(A=\sqrt{5+\sqrt{21}}+\sqrt{5-\sqrt{21}}\)
\(A^2=\left(\sqrt{5+\sqrt{21}}^2+2\sqrt{\left(5+\sqrt{21}\right)\left(5-\sqrt{21}\right)}+\sqrt{5-\sqrt{21}}^2\right)\)
\(A^2=5+\sqrt{21}+\sqrt{4\left(5+\sqrt{21}\right)\left(5-\sqrt{21}\right)}+5-\sqrt{21}\)
\(A^2=10+\sqrt{4.\left(25-21\right)}\)
\(A^2=10+\sqrt{4.4}=10+4=14\)
\(A=\sqrt{14}\)
Tương tự
16 tháng 9 2019
a) \(\sqrt{x-1}+\sqrt{2x-1}=5\)
\(\Leftrightarrow3x-2+2\sqrt{\left(x-1\right)\left(2x-1\right)}=25\)
\(\Leftrightarrow2\sqrt{\left(x-1\right)\left(2x-1\right)}=25-3x+2\)
\(\Leftrightarrow2\sqrt{\left(x-1\right)\left(2x-1\right)}=-3x+27\)
Bình phương 2 vế, ta được:
\(\Leftrightarrow4\left(x-1\right)\left(2x-1\right)=9\left(x-9\right)^2\)
\(\Leftrightarrow8x^2-4x-8x+4=9x^2-162x+729\)
\(\Leftrightarrow8x^2-12x+4-9x^2+162x-729=0\)
\(\Leftrightarrow-x^2+150x-725=0\)
\(\Leftrightarrow x^2-150x+725=0\)
\(\Leftrightarrow\left(x-145\right)\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-145=0\\x-5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=145\left(ktm\right)\\x=5\left(tm\right)\end{cases}}\)
\(\Rightarrow x=5\)
b) \(x+\sqrt{2x-1}-2=0\)
\(\Leftrightarrow\sqrt{2x-1}=2-x\)
Bình phương 2 vế, ta được:
\(\Leftrightarrow2x-1=4-4x^2+x^2=0\)
\(\Leftrightarrow2x-1-4+4x-x^2=0\)
\(\Leftrightarrow6x-5-x^2=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-5=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=5\left(ktm\right)\\x=1\left(tm\right)\end{cases}}\)
4 tháng 9 2016
1. \(\sqrt{7+2\sqrt{10}}-\sqrt{7-2\sqrt{10}}=\sqrt{\left(\sqrt{5}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}\\ =\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}=2\sqrt{2}\)
2. \(\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}=\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(2\sqrt{3}-3\right)^2}\\ =3-\sqrt{3}+2\sqrt{3}-3=\sqrt{3}\)
3. \(\sqrt{33-12\sqrt{6}}+\sqrt{15-6\sqrt{6}}=\sqrt{\left(2\sqrt{6}-3\right)^2}+\sqrt{\left(3+\sqrt{6}\right)^2}\\ =2\sqrt{6}-3+3+\sqrt{6}=3\sqrt{6}\)
4 tháng 9 2016
1.\(\sqrt{7+2\sqrt{10}}-\sqrt{7-2\sqrt{10}}=\sqrt{\left(\sqrt{2}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}\)
\(=\sqrt{5}+\sqrt{2}-\left(\sqrt{5}-\sqrt{2}\right)=2\sqrt{2}\)
2. \(\sqrt{12-6\sqrt{3}+\sqrt{21-12\sqrt{3}}}=\sqrt{12-6\sqrt{3}+\sqrt{\left(3-2\sqrt{3}\right)^2}}\)
\(=\sqrt{12-6\sqrt{3}+2\sqrt{3}-3}=\sqrt{9-4\sqrt{3}}\)
3. \(\sqrt{33-12\sqrt{6}}+\sqrt{15-6\sqrt{6}}=\sqrt{\left(2\sqrt{6}-3\right)^2}+\sqrt{\left(\sqrt{6}-3\right)^2}\)
\(=2\sqrt{6}-3+3-\sqrt{6}=\sqrt{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2019
Bài 1:
a/ ĐKXĐ: \(x\ge1\)
\(\Leftrightarrow\sqrt{x-1}-2+\sqrt{2x-1}-3=0\)
\(\Leftrightarrow\frac{x-5}{\sqrt{x-1}+2}+\frac{2\left(x-5\right)}{\sqrt{2x-1}+3}=0\)
\(\Leftrightarrow\left(x-5\right)\left(\frac{1}{\sqrt{x-1}+2}+\frac{2}{\sqrt{2x-1}+3}\right)=0\)
\(\Rightarrow x=5\)
b/ĐKXĐ:...
\(x-1+\sqrt{2x-1}-1=0\)
\(\Leftrightarrow x-1+\frac{2\left(x-1\right)}{\sqrt{2x-1}+1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(1+\frac{2}{\sqrt{2x-1}+1}\right)=0\)
\(\Rightarrow x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 9 2019
Bài 2:
\(A=\sqrt{\left(2-\sqrt{3}\right)^2}-\sqrt{\left(2+\sqrt{3}\right)^2}\)
\(=\left|2-\sqrt{3}\right|-\left|2+\sqrt{3}\right|\)
\(=2-\sqrt{3}-2-\sqrt{3}=-2\sqrt{3}\)
\(B=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)
\(=\left(3-\sqrt{6}\right)+\left(2\sqrt{6}-3\right)\)
\(=\sqrt{6}\)
\(C=\left(\frac{3+\sqrt{5}-3+\sqrt{5}}{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\right).\frac{\left(\sqrt{5}-1\right)}{\sqrt{5}\left(\sqrt{5}-1\right)}\)
\(=\frac{2\sqrt{5}}{4}.\frac{1}{\sqrt{5}}=\frac{1}{2}\)
4 tháng 7 2018
\(1.A=\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}=\dfrac{1}{2}\sqrt{\dfrac{1}{3}.144}-2\sqrt{\dfrac{1}{3}.225}-\sqrt{\dfrac{1}{3}.9}+5\sqrt{\dfrac{4}{3}}=6\sqrt{\dfrac{1}{3}}-30\sqrt{\dfrac{1}{3}}-3\sqrt{\dfrac{1}{3}}+10\sqrt{\dfrac{1}{3}}=-17\sqrt{\dfrac{1}{3}}\) \(2.B=\left(2\sqrt{27}-3\sqrt{48}+3\sqrt{75}-\sqrt{192}\right)\left(1-\sqrt{3}\right)=\left(6\sqrt{3}-12\sqrt{3}+15\sqrt{3}-8\sqrt{3}\right)\left(1-\sqrt{3}\right)=\sqrt{3}\left(1-\sqrt{3}\right)=\sqrt{3}-3\) \(3.C=\left(2\sqrt{7}-2\sqrt{6}\right).\sqrt{6}-\sqrt{168}=2\sqrt{42}-12-2\sqrt{42}=-12\) \(4.D=\left(\sqrt{28}-2\sqrt{8}+\sqrt{7}\right).\sqrt{7}+4\sqrt{14}=\left(3\sqrt{7}-4\sqrt{2}\right)\sqrt{7}=21-4\sqrt{14}+4\sqrt{14}=21\)
17 tháng 7 2017
a, \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
= \(2\sqrt{3}-10\sqrt{3}-\dfrac{\sqrt{3}\cdot\sqrt{11}}{\sqrt{11}}+5\sqrt{\dfrac{4}{3}}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\sqrt{\dfrac{12}{3^2}}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+5\dfrac{2\sqrt{3}}{3}\)
= \(2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{10\sqrt{3}}{3}\)
= \(-9\sqrt{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-27\sqrt{3}}{3}+\dfrac{10\sqrt{3}}{3}=\dfrac{-17\sqrt{3}}{3}\)
b, \(\sqrt{150}+\sqrt{1,6}\cdot\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
= \(5\sqrt{6}+\dfrac{2\sqrt{10}}{5}\cdot2\sqrt{15}+4,5\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+4,5\sqrt{\dfrac{24}{3^2}}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+4,5\cdot\dfrac{2\sqrt{6}}{3}-\sqrt{6}\)
= \(5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}=11\sqrt{6}\)
17 tháng 7 2017
c, \(\left(\sqrt{28}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\)
= \(\left(2\sqrt{7}-2\sqrt{3}+\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\)
= \(\left(3\sqrt{7}-2\sqrt{3}\right)\cdot\sqrt{7}+2\sqrt{21}\)
= \(21-2\sqrt{21}+2\sqrt{21}=21\)
d, \(\left(\sqrt{6}+\sqrt{5}\right)^2-\sqrt{120}\)
= \(6+2\sqrt{30}+5-2\sqrt{30}=11\)
12 tháng 10 2019
a) \(\left(\sqrt{27}-\sqrt{12}-\sqrt{108}-\sqrt{192}\right):\sqrt{3}=\left(3\sqrt{3}-2\sqrt{3}-6\sqrt{3}-8\sqrt{3}\right):\sqrt{3}=\left(-13\sqrt{3}\right):\sqrt{3}=-13\sqrt{3}.\frac{1}{\sqrt{3}}=-13\)
c) \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}=\left|3-\sqrt{6}\right|+\left|2\sqrt{6}-3\right|=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
VH
12 tháng 10 2019
a, \(=\left(3\sqrt{3}-2\sqrt{3}-6\sqrt{3}-8\sqrt{3}\right):\sqrt{3}\)
\(=\frac{-13\sqrt{3}}{\sqrt{3}}=-13\)
b, \(=\frac{\sqrt{2}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}.\frac{3+2\sqrt{7}}{1+\sqrt{3}}\)
\(=\frac{\sqrt{2}\left(3+2\sqrt{7}\right)}{1+\sqrt{3}}\)
c, \(=\sqrt{6-6\sqrt{6} +9}+\sqrt{24-2.2\sqrt{6}.3+9}\)
\(=\sqrt{\left(\sqrt{6}-3\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)
\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
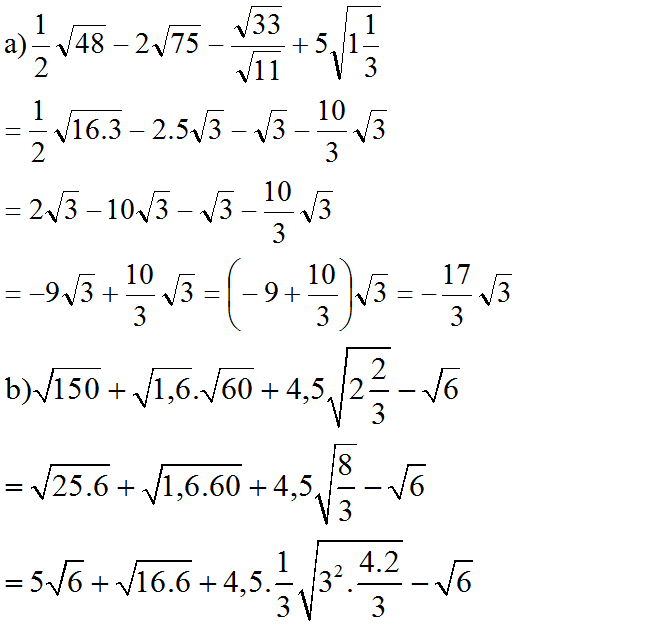
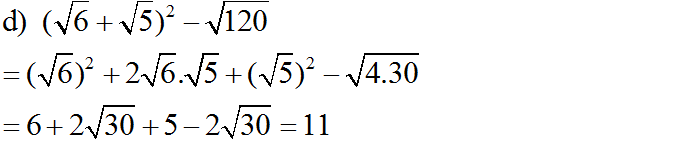
\(A=\sqrt{7+\sqrt{33}}+\sqrt{7-\sqrt{33}}>0\)
\(\Rightarrow A^2=14+2\sqrt{7^2-33}\)
\(\Rightarrow A^2=14+2\sqrt{16}=22\)
\(\Rightarrow A=\sqrt{22}\)