- . Một điều tra viên được nhờ xem xét bản di chúc sau khi người nhận bản di chúc này nghi ngờ có vấn đề. Anh ta đã nhanh chóng phát hiện ra đây là bản di chúc giả. Tại sao vậy?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

16 tháng 2 2020
1. a) Tập xác định: D = R;
y' = 3 – 2x => y' = 0 ⇔ x = 3/2
Ta có Bảng biến thiên:

Hàm số đồng biến trên khoảng (-∞; 3/2); nghịch biến trên khoảng (3/2; +∞).
b) Tập xác định: D = R;
y' = x2 + 6x – 7 => y' = 0 ⇔ x = 1, x = -7.
Bảng biến thiên:

Hàm số đồng biến trên các khoảng (-∞; -7), (1; +∞); nghịch biến trên các khoảng (-7; 1).
c) Tập xác định: D = R.
y' = 4x3 – 4x = 4x(x2 – 1) => y' = 0 ⇔ x = -1, x = 0, x = 1.
Bảng biến thiên: (Học sinh tự vẽ)
Hàm số đồng biến trên các khoảng (-1; 0), (; +∞); nghịch biến trên các khoảng (-∞; -1), (0; 1).
d) Tập xác định: D = R.
y' = -3x2 + 2x => y' = 0 ⇔ x = 0, x = 2/3.
Bảng biến thiên:

Hàm số đồng biến trên khoảng (0; 2/3); nghịch biến trên các khoảng (-∞; 0), (2/3; +∞).

TD
7 tháng 5 2021
Đặt 2x=A suy ra 4x=A2.
Do đó 4x+4-x=23 \(\Leftrightarrow\)A2+\(\frac{1}{A^2}\)=(A+\(\frac{1}{A}\))2-2=23
Do đó 2X+2-X=A+1/A=\(\sqrt{23+2}\)=5(Do A dương)
HK
8 tháng 5 2021
đặt \(t=4^x\)
\(\Rightarrow t+\frac{1}{t}=23\)
\(\Leftrightarrow t^2-23t+1=0\)
\(\orbr{\begin{cases}t=\frac{23+5\sqrt{21}}{2}\\t=\frac{23-5\sqrt{21}}{2}\end{cases}}\)
Vậy \(4^x=\frac{23+5\sqrt{21}}{2}\)hoặc \(4^x=\frac{23-5\sqrt{21}}{2}\)
\(\Rightarrow log_4\left(4^x\right)=log_4\left(\frac{23+5\sqrt{21}}{2}\right)\)
\(x=log_4\left(23+5\sqrt{21}\right)-log_4\left(2\right)\)
\(\Rightarrow2^{log_4\left(\frac{23+5\sqrt{21}}{2}\right)}+2^{-log_4\left(\frac{23+5\sqrt{21}}{2}\right)}\)
=5 :)) tự bấm máy tính nếu cần giải tay thì alo mình

16 tháng 9 2021
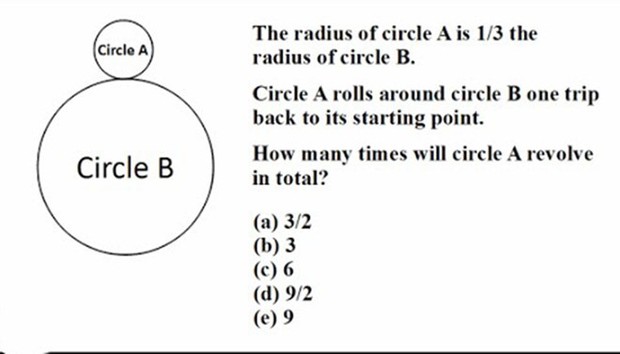
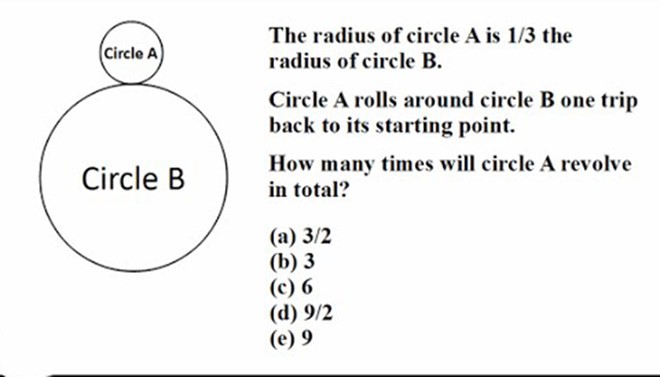
Quãng đường mà hình tròn A lăn được bằng quãng đường di chuyển của tâm hình tròn A.
Tâm I của hình tròn A cách tâm hình tròn B một khoảng bằng 4 lần bán kính của hình tròn A (tương ứng, chu vi của đường tròn mà I vạch nên cũng gấp 4 lần chu vi hình A).
Vì vậy, hình A phải thực hiện 4 vòng quay mới trở lại điểm xuất phát.
Thế nên chả có đáp án nào đúng cả

18 tháng 5 2021
Vì tờ số 3 là số la mã còn số còn lại là stn đúng ko
18 tháng 5 2021
Ha Hok tra Loi Nua Dau De coi Cac Ban Dung Hok
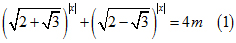 với m là tham số.
với m là tham số.

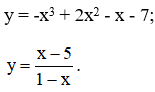 các bạn nào lớp 1 đến 11 thì không nên làm nhé
các bạn nào lớp 1 đến 11 thì không nên làm nhé
1) TXĐ: \(D=ℝ\)
\(9^x+3.6^x=4^{x+1}\)
\(\Leftrightarrow9^x-4.4^x+3.6^x=0\)
\(\Leftrightarrow\dfrac{9^x}{4^x}-4+3.\dfrac{6^x}{4^x}=0\)
\(\Leftrightarrow\left(\dfrac{9}{4}\right)^x+3\left(\dfrac{6}{4}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^2\right]^x+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x\right]^2+3\left(\dfrac{3}{2}\right)^x-4=0\)
\(\Leftrightarrow\left[\left(\dfrac{3}{2}\right)^x-1\right]\left[\left(\dfrac{3}{2}\right)^x+4\right]=0\)
\(\Leftrightarrow\left(\dfrac{3}{2}\right)^x=1\) (vì \(\left(\dfrac{3}{2}\right)^x>0\))
\(\Leftrightarrow x=0\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{0\right\}\)
2)
a) \(D=ℝ\)
Với \(m=1\) thì (1) thành:
\(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}=4\)
Để ý rằng \(\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=1\) \(\Leftrightarrow\sqrt{2-\sqrt{3}}=\dfrac{1}{\sqrt{2+\sqrt{3}}}\)
Do đó pt \(\Leftrightarrow\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\dfrac{1}{\sqrt{2+\sqrt{3}}}\right)^{\left|x\right|}-4=0\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì pt thành:
\(t+\dfrac{1}{t}-4=0\)
\(\Leftrightarrow t^2-4t+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2+\sqrt{3}\left(nhận\right)\\t=2-\sqrt{3}\left(loại\right)\end{matrix}\right.\)
Vậy \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=2+\sqrt{3}\)
\(\Leftrightarrow\left|x\right|=2\)
\(\Leftrightarrow x=\pm2\)
Vậy tập nghiệm của pt đã cho là \(S=\left\{\pm2\right\}\)]
2b) Đặt \(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\left(\sqrt{2-\sqrt{3}}\right)^{\left|x\right|}\)
\(f\left(x\right)=\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}+\dfrac{1}{\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}}\)
Đặt \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\left(t\ge1\right)\) thì \(f\left(x\right)=g\left(t\right)=t+\dfrac{1}{t}\)
\(g'\left(t\right)=1-\dfrac{1}{t^2}\ge0,\forall t\ge1\)
Lập BBT, ta thấy để \(g\left(t\right)=4m\) có nghiệm thì \(t\ge1\). Tuy nhiên, với \(t>1\) thì sẽ có 2 số \(x\) thỏa mãn \(\left(\sqrt{2+\sqrt{3}}\right)^{\left|x\right|}=t\) (là \(\log_{\sqrt{2+\sqrt{3}}}t\)
và \(-\log_{\sqrt{2+\sqrt{3}}}t\))
Với \(t=1\), chỉ có \(x=0\) là thỏa mãn. Như vậy, để pt đã cho có nghiệm duy nhất thì \(t=1\)
\(\Leftrightarrow m=g\left(1\right)=2\)
Vậy \(m=2\)