Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-b}{2a}=\dfrac{-1}{2}\\y=-\dfrac{b^2-4ac}{4a}=-\dfrac{1^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{1+8}{4}=-\dfrac{9}{4}\end{matrix}\right.\)
Vì (P): \(y=x^2+x-2\) có a=1>0
nên (P) đồng biến khi x>-1/2 và nghịch biến khi x<-1/2
Vẽ (P): 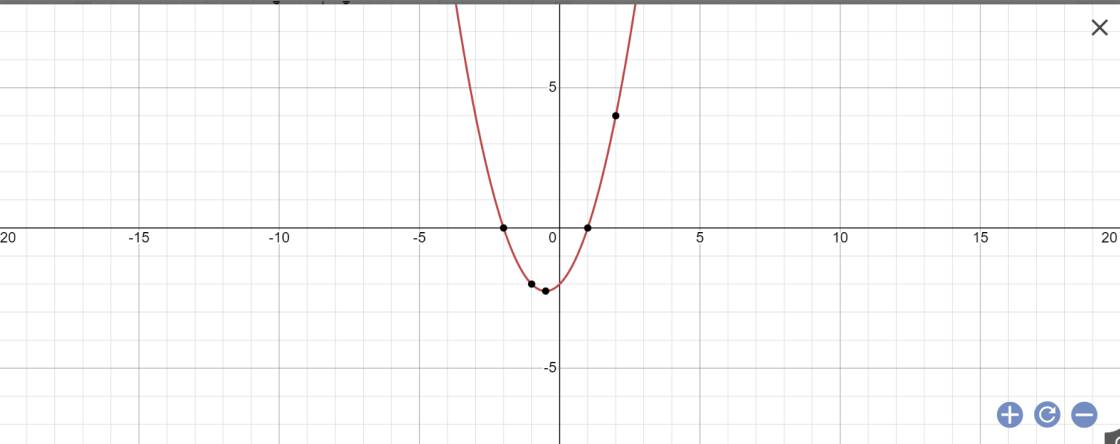
b: Phương trình hoành độ giao điểm là:
\(x^2+x-2=-\left(m+1\right)x+m+2\)
=>\(x^2+x-2+\left(m+1\right)x-m-2=0\)
=>\(x^2+\left(m+2\right)x-m-4=0\)(1)
Để (P) cắt (d) tại hai điểm phân biệt A,B nằm về hai phía so với trục Oy thì phương trình (1) có hai nghiệm phân biệt trái dấu
=>-m-4<0
=>-m<4
=>m>-4
mà \(m\in Z;m\in\left[-10;4\right]\)
nên \(m\in\left\{-3;-2;-1;0;1;2;3;4\right\}\)
=>Có 8 số thỏa mãn

\(y=ax+b\left(d\right)\)
1.
\(\left(d\right)\) đi qua \(C\left(4;-3\right)\Rightarrow4a+b=-3\)
\(\left(d\right)\) song song với \(y=-\frac{2}{3}x+1\Rightarrow\left\{{}\begin{matrix}a=-\frac{2}{3}\\b\ne1\end{matrix}\right.\)
Khi đó ta có \(\left\{{}\begin{matrix}4a+b=-3\\a=-\frac{2}{3}\\b\ne1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-\frac{2}{3}\\b=-\frac{1}{3}\end{matrix}\right.\Rightarrow y=-\frac{2}{3}x-\frac{1}{3}\left(d\right)\)
2.
Ta có \(\left\{{}\begin{matrix}a+b=2\\a=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=2\end{matrix}\right.\Rightarrow y=2x\left(d\right)\)
3.
Ta có \(\left\{{}\begin{matrix}4a+b=2\\a.\left(-\frac{1}{2}\right)=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-6\\a=2\end{matrix}\right.\Rightarrow y=2x-6\left(d\right)\)

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

a/ \(\left\{{}\begin{matrix}a=3\\2a+b=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=-1\end{matrix}\right.\) \(\Rightarrow y=3x-1\)
b/ \(\left\{{}\begin{matrix}a.1=-1\\-2a+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=-2\end{matrix}\right.\) \(\Rightarrow y=-x-2\)
c/ \(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{5}{3}\\b=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow y=-\frac{5}{3}x+\frac{1}{3}\)
d/ Thay \(x=-1;2\) vào pt (P) ta được tọa độ \(\left\{{}\begin{matrix}A\left(-1;1\right)\\B\left(2;4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow y=x+2\)

a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4a=-28\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-13\end{matrix}\right.\)
b: Vì (d)//y=-2/3x+1 nên a=-2/3
Vậy: (d): y=-2/3x+b
Thay x=4 và y=-3 vào (d), ta được:
b-8/3=-3
hay b=-1/3

mình nghĩ pt (P) : y = ax^2 - bx + c chứ ?
a, (P) đi qua điểm A(0;-1) <=> \(c=-1\)
(P) đi qua điểm B(1;-1) <=> \(a-b+c=-1\)(1)
(P) đi qua điểm C(-1;1) <=> \(a+b+c=1\)(2)
Thay c = -1 vào (1) ; (2) ta được : \(a-b=0;a+b=2\Rightarrow a=1;b=1\)
Vậy pt Parabol có dạng \(x^2-x-1=y\)
Bài 1b
(P) đi qua điểm A(8;0) <=> \(64a-8b+c=0\)
(P) có đỉnh I(6;12) \(\Rightarrow\hept{\begin{cases}-\frac{b}{2a}=6\\36a-6b+c=-12\end{cases}}\Rightarrow a=3;b=-36;c=96\)
Vậy pt Parabol có dạng : \(9x^2+36x+96=y\)
tương tự nhé