Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Dây thứ nhất có: l 1 = 100m, S 1 = 1 m m 2 , R 1 = 1,7Ω
Dây thứ hai có: l 2 = 200m, S 2 = ?, R 2 = 17Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 2 =200m nhưng lại có tiết diện S 3 = S 1 = 1 m m 2 .
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện nhưng khác chiều dài.
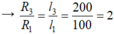
→ R 3 = 2 . R 1 = 3,4Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện.
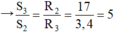
→ S 2 = S 3 / 5 = 1/5 = 0,2 m m 2

chọn dây đồng thứ 3 có S3=S1, có l3=l2
xét dây thứ nhất: \(=>\dfrac{R1}{R3}=\dfrac{l1}{l3}=>\dfrac{160}{R3}=\dfrac{100}{300}=>R3=480\Omega\)
xét dây thứ 2: \(=>\dfrac{R2}{R3}=\dfrac{S3}{S2}=>\dfrac{40}{480}=\dfrac{0,2}{S2}=>S2=2,4mm^2\)

\(R_1=\rho\dfrac{l_1}{S_1}\Rightarrow\rho=\dfrac{R_1.S_1}{l_1}=\dfrac{160.0,2.10^{-6}}{100}=3,2.10^{-7}\left(\Omega.m\right)\)
\(R_2=\rho\dfrac{l_2}{S_2}\Rightarrow S_2=\dfrac{\rho.l_2}{R_2}=\dfrac{3,2.10^{-7}.300}{40}=2,4.10^{-6}\left(m^2\right)\)

Dây thứ nhất có: l 1 = 200m, S 1 = 1 m m 2 , R 1 = 5,6Ω
Dây thứ hai có: l 2 = ? m, S 2 = 2 m m 2 , R 2 = 16,8 Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 1 = 200m nhưng lại có tiết diện S 3 = S 2 = 2 m m 2 .
Như vậy dây 1 và dây 3 có cùng vật liệu và chiều dài, khác tiết diện
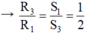
→ R 3 = R 1 /2 = 2,8Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng tiết diện, khác chiều dài
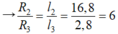
→ l 2 = 6 l 1 = 6.200 = 1200m

\(R_2=\rho\dfrac{l_2}{S_2}\Rightarrow\rho=\dfrac{R_2.S_2}{l_2}=\dfrac{8.0,1.10^{-6}}{10}=8.10^{-8}\left(\Omega.m\right)\)
\(R_1=\rho\dfrac{l_1}{S_1}=8.10^{-8}.\dfrac{20}{0,4.10^{-6}}=4\left(\Omega\right)\)

Vì 2 dây cùng chất liệu và cùng độ dài
Nên
\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}\Rightarrow R_2=\dfrac{R_1S_1}{S_2}=\dfrac{0,2\cdot0,4}{0,1}=0,8\left(\Omega\right)\)


Tóm tắt
\(l_1=100m\\ S_1=1mm^2\\ R_1=1,7\Omega\\ l_2=200m\\ R_2=17\Omega\)
__________
\(S_2=?mm^2\)
Giải
Vì R tỉ lệ thuận với l và tỉ lệ nghịch với S
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}\cdot\dfrac{S_2}{S_1}\\ \Leftrightarrow\dfrac{1,7}{17}=\dfrac{100}{200}\cdot\dfrac{S_2}{1}\\ \Leftrightarrow S_2=0,2mm^2\)