Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

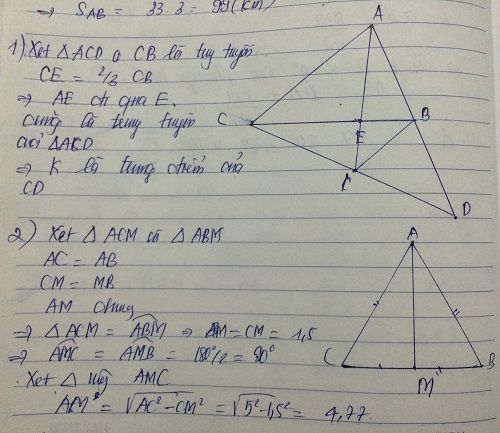
ai giup minh cau 2a khg
chiu nay co kiem tra rui
giup minh vs![]()
![]()
![]()

a/ Áp dụng định lí Pytago vào tam giác vuông ABC ta được:
BC^2=AB^2+AC^2=3^2+4^2=5^2
=> BC=5 cm
b)c/m tam giác BAM= tam giác CDM=><ABC=<DCB mà 2 góc này là 2 góc so le trong=>AB//DC
VÌ tam giác BAM= tam giác CDM=> AB=CD

A B C D E I
a, Áp dụng định lý Pytago vào tam giác vuông ABC có:
AB2 + AC2 = BC2
92 + AC2 = 152
81 + AC2 = 225
AC2 = 225 - 81
AC2 = 144
AC = 12 (cm)
Xét tam giác ABC có: AB < AC < BC.
nên góc ACB < ABC < BAC ( đối diện với góc lớn hơn là cạnh lớn hơn )
b,do A là trung điểm BD (gt)
nên AB=DB
nên CA là đg trung tuyến.
Xét tam giác BCD có: CA vuông góc AB nên CA là đg cao
mà CA là đg trung tuyến.
nên tam giác BCD cân tại C
c,...

Ta có tam giác ABC cân tại A nên góc B=góc C mà góc ABC+ABD=180 độ
góc ACB+ACE=180 độ
=> góc ABD=góc ACE
Xét tam giác ABD và tam giác ACE có
AB=AC (tam giác ABC cân tại A)
góc ABD=góc ACE (cmt)
BD=CE(gt)
=> tam giác ABD=tam giác ACE(c-g-c)
=> AD=AE(cạnh tương ứng)
Vậy tam giác ADE cân và cân tại A
b/ Ta có tam giác ADE là tam giác cân và cân tại A nên góc D=góc E
Xét tam giác AMD và tam giác AME có:
AD=AE(tam giác ADE cân tại A)
góc D=góc E(cmt)
góc AMD=góc AME=90 độ
=> tam giác AMD=tam giác AME(ch-gn)
=> góc DAM=góc EAM(góc tương ứng)
Vậy AM là tia phân giác góc DAE

A B C D E M I
a) Ta có : \(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{CBD}=180^o\\\widehat{ACB}+\widehat{BCE}=180^o\end{matrix}\right.\left(kềbù\right)\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) cân tại A)
Nên : \(180^o-\widehat{ABC}=180^o-\widehat{ACB}\)
\(\Leftrightarrow\widehat{CBD}=\widehat{BCE}\)
Xét \(\Delta BDC,\Delta CBE\) có :
\(BC:Chung\)
\(\widehat{CBD}=\widehat{BCE}\left(cmt\right)\)
\(BD=CE\left(gt\right)\)
=> \(\Delta BDC=\Delta CBE\left(c.g.c\right)\)
Xét \(\Delta BID,\Delta CIE\) có :
\(\widehat{BID}=\widehat{CIE}\) (đối đỉnh)
\(BD=CE\left(gt\right)\)
\(\widehat{BDI}=\widehat{CEI}\) (do \(\Delta BDC=\Delta CBE\))
=> \(\Delta BID=\Delta CIE\left(g.c.g\right)\)
=> \(\left\{{}\begin{matrix}IB=IC\left(\text{2 cạnh tương ứng}\right)\\ID=IE\left(\text{2 cạnh tương ứng}\right)\end{matrix}\right.\)
b) Ta có : \(\left\{{}\begin{matrix}AB=AC\left(\text{tam giác ABC cân tại A}\right)\\BD=CE\left(gt\right)\end{matrix}\right.\)
Lại có : \(\left\{{}\begin{matrix}AB+BD=AD\\AC+CE=AE\end{matrix}\right.\)
Suy ra : \(AB+BD=AC+EC\)
\(\Leftrightarrow AD=AE\)
=> \(\Delta ADE\) cân tại A
Ta có : \(\widehat{ADE}=\widehat{AED}=\dfrac{180^o-\widehat{A}}{2}\left(1\right)\)
Xét \(\Delta ABC\) cân tại A có :
\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^{^O}-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{ABC}\left(=\dfrac{180^{^O}-\widehat{A}}{2}\right)\)
Mà thấy : 2 góc này ở vị trí đồng vị
=> \(BC//DE\rightarrowđpcm\)
c) Xét \(\Delta ABM,\Delta ACM\) có :
\(AB=AC\) (\(\Delta ABC\) cân tại A)
\(\widehat{ABM}=\widehat{ACM}\) (\(\Delta ABC\) cân tại A)
BM = CM (M là trung điểm của BC)
=> \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> AM là tia phân giác của \(\widehat{A}\) (3)
Ta chứng minh : \(\Delta ABI=\Delta ACI\)
Suy ra : \(\widehat{AIB}=\widehat{AIC}\) (2 góc tương ứng)
=> AI là tia phân giác của \(\widehat{A}\) (4)
Từ (3) và (4) => \(AM\equiv AI\)
=> A, M, I thẳng hàng.
=> đpcm
 10 K NHA !
10 K NHA !
giup minh voi. mai co tiet rui