Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chiều cao của hình thang là :
40 x 2 : 5 = 16 ( cm )
Diện tích của hình thang là :
( 27 + 48 ) x 16 : 2 = 600 ( cm2 )
đáp số : 600 cm2
Chiều cao của hình thang là:
40.2 : 5 = 16 (cm)
Diện tích hình thang là:
(27 + 48) .16 : 2 = 600 (cm2)
Đáp số: 600 cm2

Đáy bé miếng bìa hình thang là:
36 x \(\frac{5}{6}\)= 30 (cm)
a) Diện tích miếng bìa là:
20 x ( \(\frac{36+30}{2}\)) = 660 (cm)
b) Tự làm

Hỏi ngu tí nha: hình thang có đáy lớn bằng đáy bé à ??? nếu thế thì còn gì là lớn và bé nữa.... không biết có phải hình bình hành hoặc là hình chữ nhật........
mình viết nhầm đó
một miếng bìa hình thang có đáy lớn 36 cm ,dáy bé bằng5/6đáy lớn, chiều cao 20cm
a) Tính diện tích miếng bìa
b)Hãy cắt miếng bìa thành 3 phần bằng nhau mà không cạnh nào của miếng bìa bị cắt(vẽ hình)

có góc ABC là góc tù vì 360-90-90-60=120
vậy CM \(\ge\)BC
vậy độ dài đoạn CM hay đọ dài vecto CM nhỏ nhất khi bằng BC
khi đó min(CM)=?
từ B hạ chân đường vuống góc xuống CD
khi đó ta dễ tính ra được BC=2a
từ C hà đường vuông góc tới AB
khi đó \(|\overrightarrow{CM}|^2\)=CM^2 = CH^2 + HM^2
vì CH không đổi nên ta không tính đến nó
có HM bé hơn hoặc bằng HA
vậy AC>= CM
vậy max(CM)=AC=\(2\sqrt{2}a\)

Gọi \(\overrightarrow{n}=\left(a,b\right)\) là vectơ pháp tuyến của CD (\(a^2+b^2\ne0\)
Ta có phương trình CD : \(ax+by+a+b=0\)
\(S_{BCD}=S_{ACD}=8\Rightarrow d\left(A;CD\right)=\frac{2.S}{CD}=2\Rightarrow d\left(M.CD\right)=1\)
\(\Rightarrow\frac{\left|2a-b\right|}{\sqrt{a^2+b^2}}=1\Leftrightarrow3a^2-4ab=0\)\(\rightarrow\begin{cases}a=0;b=1\\a=4;b=3\end{cases}\)\(\rightarrow\begin{cases}CD:y+1=0\\CD:4x+3y+7=0\end{cases}\)
Với \(CD:y+1=0\rightarrow D\left(d;-1\right);CD^2=4.AB^2=64\Leftrightarrow\begin{cases}d=7\\d=-9:L\end{cases}\)
\(D\left(7;-1\right);\overrightarrow{AB}=\frac{1}{2}\overrightarrow{DC}=\left(-4;0\right)\rightarrow B\left(-9;-3\right)\)
Với \(CD:4x+3y+7=0\rightarrow D\left(d;\frac{-4d-7}{3}\right)\rightarrow CD^2=\frac{25\left(d+1\right)^2}{9}=64\) (loại)

Ta có : \(\widehat{AOD}=\widehat{BOC}\) (hai góc đối đỉnh)
\(\Rightarrow\widehat{DAO}=\widehat{BOC}\) (so le trong)
\(\Rightarrow\Delta BOC=\Delta AOD\Rightarrow S_{BOC}=S_{AOD}\)

Chọn C.
Do I là trung điểm của DC nên ta có:
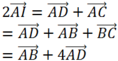
Lại có:
![]()
suy ra
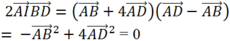
Vậy AI ⊥ BD.
a: AB=20cm; AH=(25+20)/2=22,5m
S=22,5^2=506,25m2
b: Xét tứ giác ABMC có
AB//MC
AB=MC
=>ABMC là hbh
=>S ABI=S CMI
c: BI/IC=1