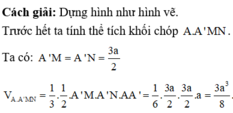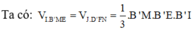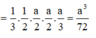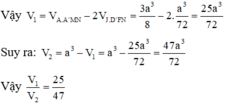Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B

Gọi x là độ dài của cạnh hình lập phương
Ta có: 

Theo giả thiết, 
![]()
Vậy thể tích lập phương là: ![]()

Đáp án B
Khối lập phương có thể tích bằng 8 nên hình lập phương có cạnh bằng 2.
Hình lập phương có 6 mặt đều là hình vuông bằng nhau nên tổng diện tích cần tìm là 6. 22 = 24.

Đáp án A
Do khối lập phương có 6 mặt bằng nhau đều là hình vuông nên ta có diện tích mỗi mặt là 9 c m 2
⇒ độ dài cạnh hình lập phương là 3cm
Từ đó ta có thể tích khối lập phương là 27 c m 3