Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7. y = f(x) = 2x2 + 3 và f(x) = 21
=> 2x2 + 3 = 21
=> 2x2 = 21 - 3= 18
=> x2 = 18 : 2
=> x2 = 9 => x = 3 hoặc x = -3
8. Điểm A(-2;3) thuộc góc phần tư thứ II của mặt phẳng tọa độ Oxy
9. y = 30x
10. B(1;-2) (bn có thể chọn điểm khác vs tạo độ khác cx đc)
11. x và y là 2 đại lượng tỉ lệ thuận
12. A(2;3)

mik sửa lại câu nha
câu 6 : Tọa độ (2017 ; -2018 ) biểu diễn điểm thuộc góc phần tư thứ mấy?
A.(I) B. (II) C. (III) D. (IV)
Câu 7 :
: Đồ thị hàm số y = a.x (a không bằng 0)luôn đi qua điểm nào:
A.(1;0) B. (0;1) C. (0;0) D. (1;1)
Câu 8 Bỏ nha

2, Ta có: f(5)= 2.5=10
3, Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ là 3 thì: y= 3x
4, ... x thì tỉ lệ nghịch với y theo hệ số tỉ lệ là: a
5, .... Ta có: xy= 60 hay x và y tỉ lệ nghịch theo hệ số tỉ lệ là: 60
6, Tọa độ của góc O trong mặt phẳng tọa độ là: (0;0)

Bài 1:
A C B
Độ dài cạnh AB: ( 49 + 7 ) : 2 = 28 (cm)
Độ dài cạnh AC: 28 - 7 = 21 (cm)
Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A có:
\(BC^2=AC^2+AB^2\)
Hay \(BC^2=21^2+28^2\)
\(\Rightarrow BC^2=441+784\)
\(\Rightarrow BC^2=1225\)
\(\Rightarrow BC=35\left(cm\right)\)
Bài 2:
A B C D
Áp dụng định lý Py-ta-go vào tam giác ABD vuông tại D có:
\(AB^2=AD^2+BD^2\)
\(\Rightarrow AD^2=AB^2-BD^2\)
Hay \(AD^2=17^2-15^2\)
\(\Rightarrow AD^2=289-225\)
\(\Rightarrow AD^2=64\)
\(\Rightarrow AD=8\left(cm\right)\)
Trong tam giác ABC có:
\(AD+DC=AC\)
\(\Rightarrow DC=AC-AD=17-8=9\left(cm\right)\)
Áp dụng định lý Py-ta-go vào tam giác BCD vuông tại D có:
\(BC^2=BD^2+DC^2\)
Hay \(BC^2=15^2+9^2\)
\(\Rightarrow BC^2=225+81\)
\(\Rightarrow BC^2=306\)
\(\Rightarrow BC=\sqrt{306}\approx17,5\left(cm\right)\)

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

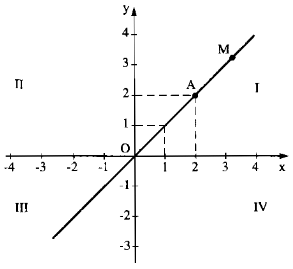
a) Điểm A có hoành độ bằng 2 thì điểm A có tung độ bằng 2.
b) Điểm M nằm trên tia phân giác của góc vuông số I và số III thì có tung độ và hoành độ bằng nhau.