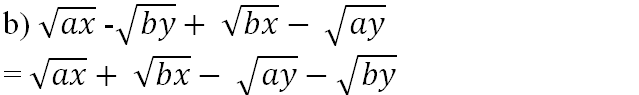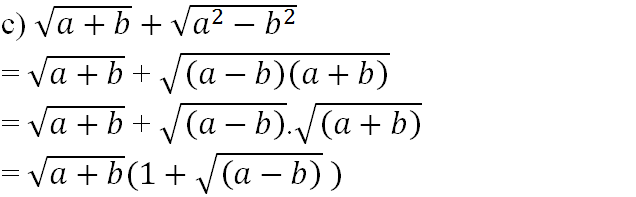Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a)\) \(xy-y\sqrt{x}+\sqrt{x}-1\)
= \(y\sqrt{x}.(\sqrt{x}-1)+\sqrt{x}-1\)
=\((\sqrt{x}-1).(y\sqrt{x}+1)\).
\(b)\)\(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}\)
=\(\sqrt{a}.\sqrt{x}-\sqrt{b}.\sqrt{y}+\sqrt{b}.\sqrt{x}-\sqrt{a}.\sqrt{y}\)
=\(\sqrt{a}.\sqrt{x}+\sqrt{b}.\sqrt{x}-\sqrt{a}.\sqrt{y}-\sqrt{b}.\sqrt{y}\)
=\(\sqrt{x}.(\sqrt{a}+\sqrt{b})-\sqrt{y}.(\sqrt{a}+\sqrt{b})\)
=\((\sqrt{x}-\sqrt{y}).(\sqrt{a}+\sqrt{b})\).
\(c)\)\(\sqrt{a+b}+\sqrt{a^2-b^2}\)
=\(\sqrt{a+b}+\sqrt{(a+b).(a-b)}\)
=\(\sqrt{a+b}+\sqrt{a+b}.\sqrt{a-b}\)
=\(\sqrt{a+b}.\left(1+\sqrt{a-b}\right)\).
\(d)\) \(12-\sqrt{x}-x\)
=\(12-4\sqrt{x}+3\sqrt{x}-x\)
=\(4.\left(3-\sqrt{x}\right)+\sqrt{x}\left(3-\sqrt{x}\right)\)
=\(\left(3-\sqrt{x}\right).\left(4+\sqrt{3}\right)\).

\(\text{a) }\sqrt{a^3+b^3}+\sqrt{a^2-b^2}=\sqrt{\left(a+b\right)\left(a^2-ab+b^2\right)}+\sqrt{\left(a+b\right)\left(a-b\right)}\)
\(=\sqrt{a+b}\left(\sqrt{a^2-ab+b^2}+\sqrt{a-b}\right)\)
\(\text{b) }\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{xy}\text{ không phân tích được.}\)
\(\text{c) }=\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)+\left(\sqrt{x}-\sqrt{y}\right).\sqrt{xy}\)
\(=\left(\sqrt{x}-\sqrt{y}\right)\left(x+y+2\sqrt{xy}\right)\)\(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)^2\)
\(\text{d) }a+5\sqrt{a}+4=\sqrt{a}.\sqrt{a}+\sqrt{a}+4\sqrt{a}+4=\sqrt{a}\left(\sqrt{a}+1\right)+4\left(\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)\left(\sqrt{a}+4\right)\)

\(A,ĐKXĐ:x;y\ge0\)
\(A=\sqrt{xy}-2\sqrt{y}-5\sqrt{x}+10\)
\(=\sqrt{y}\left(\sqrt{x}-2\right)-5\left(\sqrt{x}-2\right)\)
\(=\left(\sqrt{x}-2\right)\left(\sqrt{y}-5\right)\)
\(ĐKXĐ:x;y\ge0\)
\(B=a\sqrt{x}+b\sqrt{y}-\sqrt{xy}-ab\)
\(=\left(a\sqrt{x}-\sqrt{xy}\right)+\left(b\sqrt{y}-ab\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)+b\left(\sqrt{y}-a\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)-b\left(a-\sqrt{y}\right)\)
\(=\sqrt{x}\left(a-\sqrt{y}\right)-b\left(a-\sqrt{y}\right)\)
\(=\left(a-\sqrt{y}\right)\left(\sqrt{x}-b\right)\)

a,\(a\sqrt{b}-b\sqrt{a}\)= \(\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)\)
b,\(x\sqrt{x}+\sqrt{x}-x-1\)
=\(\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)-\(\sqrt{x}\left(\sqrt{x}-1\right)\)
=\(\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1-\sqrt{x}\right)\)
=\(\left(\sqrt{x}-1\right)\left(x+1\right)\)
c,\(\sqrt{ab}+2\sqrt{a}+3\sqrt{b}+6\)=\(\sqrt{a}\left(\sqrt{b}+2\right)\)+\(3\left(\sqrt{b}+2\right)\)
=\(\left(\sqrt{b}+2\right)\left(3+\sqrt{a}\right)\)
d,\(\sqrt{ax}-\sqrt{by}+\sqrt{bx}-\sqrt{ay}\)
=\(\sqrt{a}\left(\sqrt{x}-\sqrt{y}\right)+\sqrt{b}\left(\sqrt{x}-\sqrt{y}\right)\)
=\(\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{a}+\sqrt{b}\right)\)

a: \(=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}-\sqrt{ab}=\sqrt{ab}-\sqrt{ab}=0\)
b: \(=\dfrac{\left(\sqrt{x}-2\sqrt{y}\right)^2}{\sqrt{x}-2\sqrt{y}}+\dfrac{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\)
\(=\sqrt{x}-2\sqrt{y}+\sqrt{y}=\sqrt{x}-\sqrt{y}\)
c: \(=\sqrt{x}+2-\dfrac{x-4}{\sqrt{x}-2}\)
\(=\sqrt{x}+2-\sqrt{x}-2=0\)

a, \(\dfrac{\sqrt{15}-\sqrt{6}}{\sqrt{35}-\sqrt{14}}=\dfrac{\sqrt{3}.\sqrt{5}-\sqrt{3}.\sqrt{2}}{\sqrt{5}.\sqrt{7}-\sqrt{7}.\sqrt{2}}\)
\(=\dfrac{\sqrt{3}.\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{7}.\left(\sqrt{5}-\sqrt{2}\right)}=\dfrac{\sqrt{3}}{\sqrt{7}}\)
b, \(\dfrac{2\sqrt{15}-2\sqrt{10}+\sqrt{6}-3}{2\sqrt{5}-2\sqrt{10}-\sqrt{3}+\sqrt{6}}\)
\(=\dfrac{2.\sqrt{5}.\sqrt{3}-2.\sqrt{2}.\sqrt{5}-\sqrt{3}.\sqrt{3}+\sqrt{2}.\sqrt{3}}{2.\sqrt{5}-2.\sqrt{2}.\sqrt{5}-\sqrt{3}+\sqrt{2}.\sqrt{3}}\)
\(=\dfrac{2\sqrt{5}\left(\sqrt{3}-\sqrt{2}\right)-\sqrt{3}.\left(\sqrt{3}-\sqrt{2}\right)}{2\sqrt{5}.\left(1-\sqrt{2}\right)-\sqrt{3}.\left(1-\sqrt{2}\right)}\)
\(=\dfrac{\left(2\sqrt{5}+\sqrt{3}\right).\left(\sqrt{3}-\sqrt{2}\right)}{\left(2\sqrt{5}-\sqrt{3}\right).\left(1-\sqrt{2}\right)}=\dfrac{\sqrt{3}-\sqrt{2}}{1-\sqrt{2}}\)
c, \(\dfrac{x+\sqrt{xy}}{y+\sqrt{xy}}=\dfrac{\sqrt{x}.\sqrt{x}+\sqrt{x}.\sqrt{y}}{\sqrt{y}.\sqrt{y}+\sqrt{x}.\sqrt{y}}\)
\(=\dfrac{\sqrt{x}.\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{y}.\left(\sqrt{x}+\sqrt{y}\right)}=\dfrac{\sqrt{x}}{\sqrt{y}}\)
Chúc bạn học tốt!!!
d) \(\dfrac{\sqrt{a}+a\sqrt{b}-\sqrt{b}-b\sqrt{a}}{ab-1}\) = \(-\dfrac{\sqrt{a}\left(1+\sqrt{ab}\right)-\sqrt{b}\left(1+\sqrt{ab}\right)}{1-ab}\)
= \(-\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(1+\sqrt{ab}\right)}{\left(1+\sqrt{ab}\right)\left(1-\sqrt{ab}\right)}\) = \(-\dfrac{\sqrt{a}-\sqrt{b}}{1-\sqrt{ab}}\) = \(\dfrac{\sqrt{b}-\sqrt{a}}{1-\sqrt{ab}}\)