Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)A=x(x+1)(x+2)(x+3)
\(=\left(x^2+3x\right)\left(x^2+3x+2\right)\)
Đặt \(t=x^2+3x\) ta đc:
\(t\left(t+2\right)\)\(=t^2+2t+1-1\)
\(=\left(t+1\right)^2-1\ge-1\)
Dấu = khi \(t=-1\Rightarrow x^2+3x=-1\)\(\Rightarrow\)\(x=\frac{-3\pm\sqrt{5}}{2}\)
Vậy MinA=-1 khi \(x=\frac{-3\pm\sqrt{5}}{2}\)
b)\(B=\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Với a,b,c dương ta áp dụng Bđt Cô si 3 số:
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\)
\(\Rightarrow\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
Dấu = khi a=b=c
Vậy MinB=9 khi a=b=c
c)\(C=a^2+b^2+c^2\)
Áp dụng Bđt Bunhiacopski 3 cặp số ta có:
\(\left(1^2+1^2+1^2\right)\left(a^2+b^2+c^2\right)\ge\left(1a+1b+1c\right)^2=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)
\(\Rightarrow3\left(a^2+b^2+c^2\right)\ge\frac{9}{4}\)
\(\Rightarrow a^2+b^2+c^2\ge\frac{3}{4}\)
\(\Rightarrow C\ge\frac{3}{4}\)
Dấu = khi \(a=b=c=\frac{1}{2}\)
Vậy MinC=\(\frac{3}{4}\) khi \(a=b=c=\frac{1}{2}\)

Câu 1:
Theo đề, ta có: \(x_1-x_2=1\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-2x_1x_2=m^2-2\cdot12=m^2-24\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1-x_2=m^2-24\\x_1-x_2=-m^2+24\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2-24=1\\-m^2+24=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m^2=25\\m^2=23\end{matrix}\right.\)
hay \(m\in\left\{5;-5;\sqrt{23};-\sqrt{23}\right\}\)

1, a)Vs a,b,c >0 ,áp dụng bđt svac-xơ có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\left(1+1+1\right)^2}{a+b+c}=\frac{9}{a+b+c}\)
<=> \(\frac{1}{a+b+c}\ge\frac{9}{a+b+c}\) (vô lý)
=>Phương trình \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\) vô nghiệm

\(a+\sqrt{1-a^2}=b+\sqrt{1-b^2}\)
\(\Rightarrow a\sqrt{1-a^2}=b\sqrt{1-b^2}\)
\(\Rightarrow a^2\left(1-a^2\right)=b^2\left(1-b^2\right)\)
\(\Rightarrow a^2-a^4=b^2-b^4\)
\(\Rightarrow a^2-b^2-\left(a^2-b^2\right)\left(a^2+b^2\right)=0\)
\(\Rightarrow\left(a^2-b^2\right)\left(a^2+b^2-1\right)=0\)
\(\Rightarrow a^2+b^2=1\)
- Với \(y=0\Rightarrow x=1\) là 1 nghiệm của pt
- Với \(y>0\Rightarrow2016^y\) luôn chẵn
\(VT=1+x\left(x^3+x^2+x+1\right)=1+x\left(x+1\right)\left(x^2+1\right)\)
Do \(x\left(x+1\right)\) là tích 2 STN liên tiếp nên luôn chẵn
\(\Rightarrow VT\) luôn lẻ \(\Rightarrow\) pt vô nghiệm
Vậy pt có cặp nghiệm duy nhất \(\left(x;y\right)=\left(0;0\right)\)
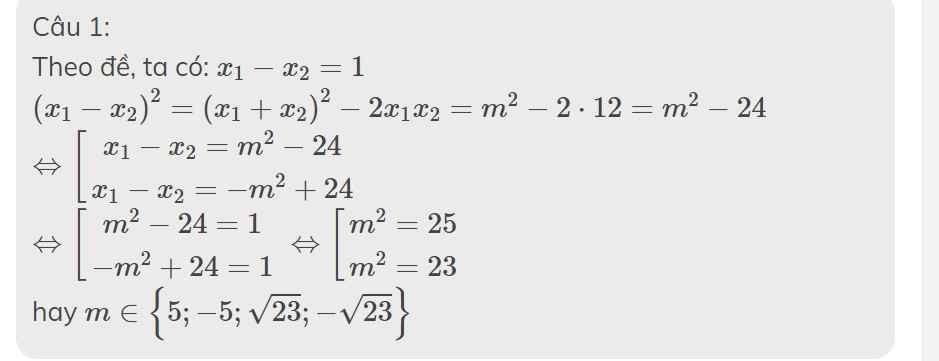
Câu A + C = C - B + A + B = B x 1,8 sai thì phải , nếu như 2 bạn trước làm thì A, B ,C là 4,5,6
A + C = C - B +A +B = B x 1,8 thay vào ko đúng
Bài 1 là 4;5;6 bài 2 k muốn suy nghĩ nên chưa làm được