
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
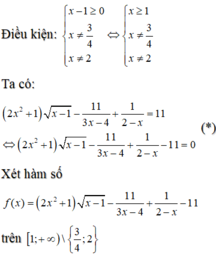
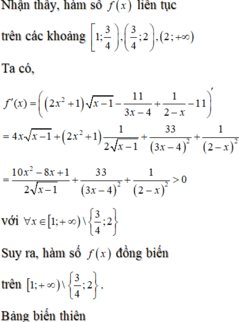
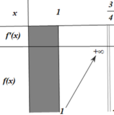
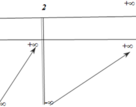
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số f(x) và trục hoành.
Từ bảng biến thiên ta suy ra: Số nghiệm của phương trình (*) bằng 2

ĐKXĐ: \(x>-3\)
Xét hàm \(f\left(x\right)=2^{x+1}+log_3\left(x+3\right)-12\)
\(f'\left(x\right)=2^{x+1}.ln2+\dfrac{1}{\left(x+3\right)ln3}>0\) ; \(\forall x>-3\)
\(\Rightarrow f\left(x\right)\) đồng biến
\(f\left(2\right)=8+log_35-12=log_35-4< 0\)
\(f\left(3\right)=4+log_36>0\)
\(\Rightarrow f\left(x\right)< 0\) có các nghiệm nguyên: \(x=\left\{-2;-1;0;1;2\right\}\)

Điều kiện:
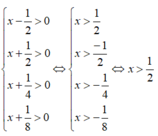
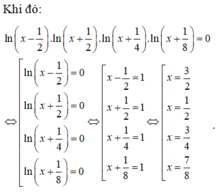
So với điều kiện, ta được tập nghiệm của phương trình là S = 3 2 ; 3 4 ; 7 8
Vậy phương trình đã cho có 3 nghiệm
Đáp án A

![]()
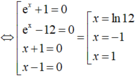
Trong đó ta thấy x=1 là nghiệm bội hai của phương trình ⇒ x=1 không là điểm cực trị của hàm số
Vậy hàm số có 2 điểm cực trị.
Chọn B


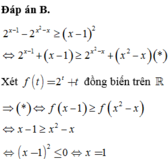
1 - 12 = -11
Cái này tính ra âm
1 - 12 = -11